ANGLE PAIRS AND TWO STEP EQUATIONS

Vertical angles are the opposite angles formed by two intersecting lines. Vertical angles are congruent because the angles have the same measure.

Adjacent angles are pairs of angles that share a vertex and one side but do not overlap.

Complementary angles are two angles whose measures have a sum of 90°.

Supplementary angles are two angles whose measures have a sum of 180°. We discovered in the Explore Activity that adjacent angles formed by two intersecting lines are supplementary.

Example 1 :

Find the measure of angle <EHF.   

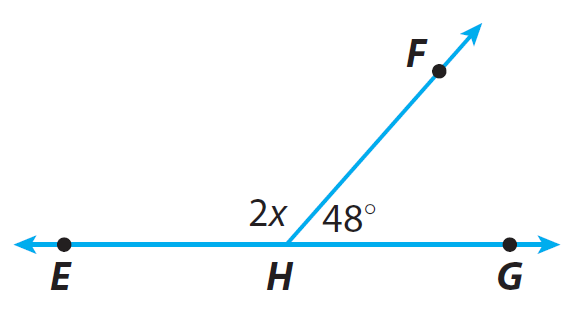
Step 1 : 

Identify the relationship between ∠EHF and ∠FHG.

Since angles ∠EHF and ∠FHG form a straight line, the sum of the measures of the angles is 180°.

∠EHF and ∠FHG are supplementary angles.

Step 2 : 

Write and solve an equation to find x. 

The sum of the measures of supplementary angles is 180°.

m∠EHF + m∠FHG  =  180°

2x + 48° = 180°

Subtract 48° from both sides. 

(2x + 48°) - 48°  =  180° - 48°

2x  =  132°

Divide both sides by 2. 

(2x) / 2  =  (132°) / 2

x  =  66° 

Step 3 : 

Find the measure of ∠EHF.

m∠EHF  =  2x

m∠EHF  =  2(66°)

m∠EHF  =  132°

Example 2 :

Find the measure of angle ∠ZXY.   

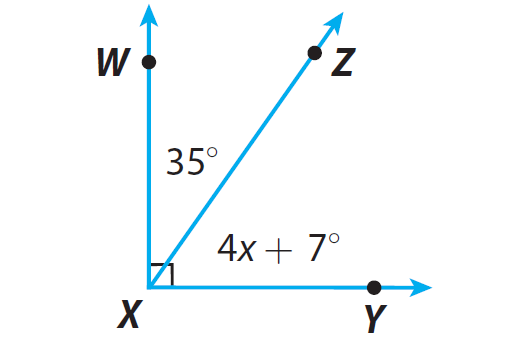
Step 1 : 

Identify the relationship between ∠WXZ and ∠ZXY.

∠WXZ and ∠ZXY are complementary angles.

Step 2 : 

Write and solve an equation to find x. 

The sum of the measures of complementary angles is 90°.

m∠WXZ + m∠ZXY  =  90°

4x + 7° + 35° = 90°

4x + 42°  =  90°

Subtract 42° from both sides. 

(4x + 42°) - 42°  =  90° - 42°

4x  =  48°

Divide both sides by 4. 

(4x) / 4  =  (48°) / 4

x  =  12° 

Step 3 : 

Find the measure of ∠EHF.

m∠ZXY  =  4x + 7°

m∠ZXY  =  4(12°) + 7°

m∠ZXY  =  48° + 7°

m∠ZXY  =  55°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.