ANGLE RELATIONSHIPS IN CIRCLES

Using Tangents and Chords

We know that the measure of an angle inscribed in a circle is half the measure of its intercepted arc.  This is true even if one side of the angle is tangent to the circle. 

Theorem :

If a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one half the measure of its intercepted arc.

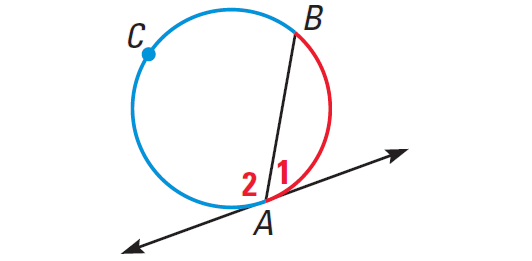
In the diagram, show above, we have 

m∠1  =  1/2 ⋅ m∠arc AB

m∠2  =  1/2 ⋅ m∠arc BCA

Finding Angle and Arc Measures

Example 1 :

Line m is tangent to the circle. Find the measure of the red angle.

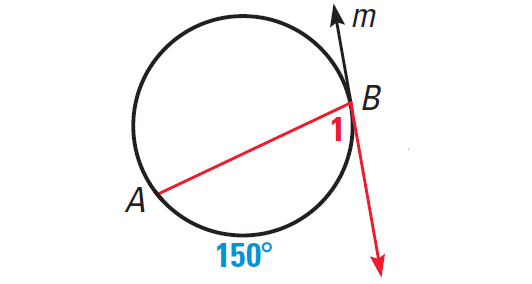
Solution :

m∠1  =  1/2 ⋅ 150°

m∠1  =  75°

Example 2 : 

Line m is tangent to the circle. Find the measure of the red arc.

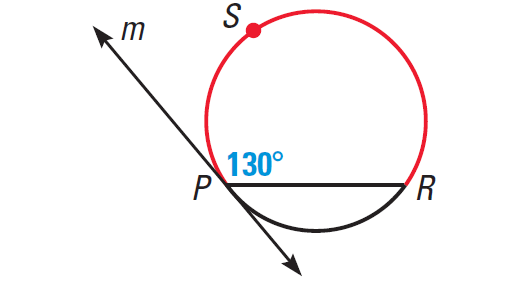
Solution :

m∠arc RSP  =  2 ⋅ 130°

m∠arc RSP  =  260°

Finding an Angle Measure

Example 3 :

In the diagram below, BC is tangent to the circle.  Find m∠CBD.

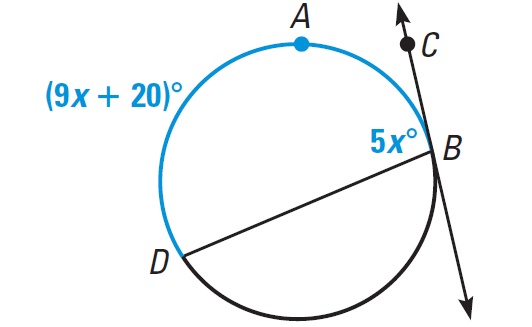
Solution :

m∠ CBD  =  1/2 ⋅ m∠arc DAB

5x  =  1/2 ⋅ (9x + 20)

Multiply each side by 2.

10x  =  9x + 20

Subtract 9x from each side.

x  =  20

So, the angle measure CBD is

m∠ CBD  =  5(20°)

m∠ CBD  =  100°

Lines Intersecting Inside or Outside a Circle

If two lines intersect a circle, there are three places where the lines can intersect.

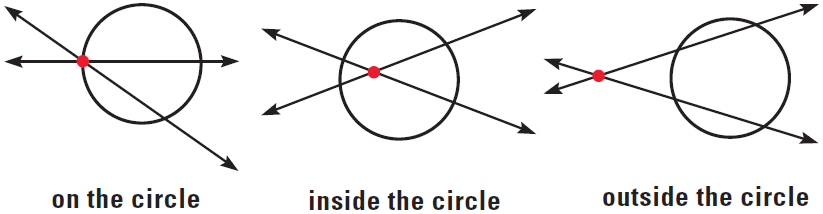
We know how to find angle and are measures when lines intersect on the circle.  We can use the following Theorems find measures when the lines intersect inside or outside the circle. 

Theorem 1 :

If two chords intersect in the interior of a circle, then the measure of each angle is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle.

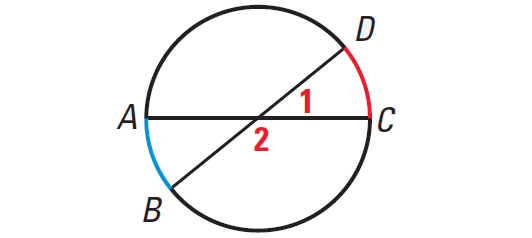
In the diagram shown above, we have

m∠1  =  1/2 ⋅ (m∠arc CD + m∠arc AB)

m∠2  =  1/2 ⋅ (m∠arc BC + m∠arc AD)

Theorem 2 :

If a tangent and a secant, two tangents, or two secants intersect in the exterior of a circle, then the measure of the angle formed is one half the difference of the measures of the intercepted arcs.

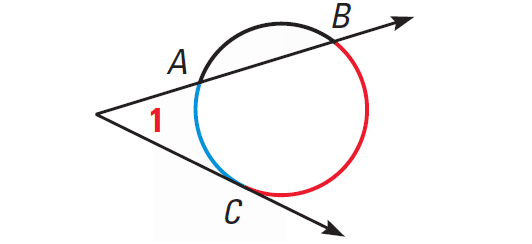
In the diagram shown above, we have

m∠1  =  1/2 ⋅ (m∠arc BC - m∠arc AC)

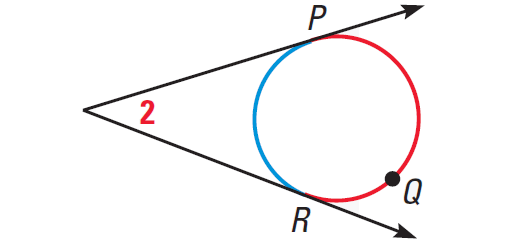
In the diagram shown above, we have

m∠2  =  1/2 ⋅ (m∠arc PQR - m∠arc PR)

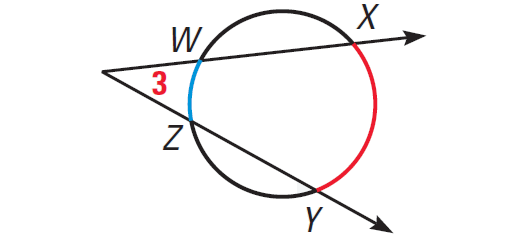
In the diagram shown above, we have

m∠3  =  1/2 ⋅ (m∠arc XY - m∠arc WZ)

Finding the Measure of an Angle Formed by Two Chords

Example 4 :

Find the value of x in the diagram shown below. 

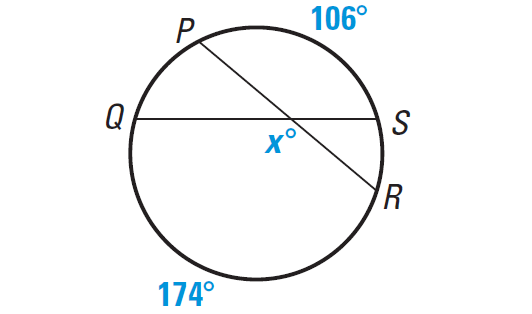
Solution :

x°  =  1/2 ⋅ (m∠arc PS + m∠arc RQ)

x°  =  1/2 ⋅ (106° + 174°)

x°  =  1/2 ⋅ (280°)

x°  =  140°

Hence, the value of x is 140. 

Using Theorem 2

Example 5 :

Find the value of x in the diagram shown below. 

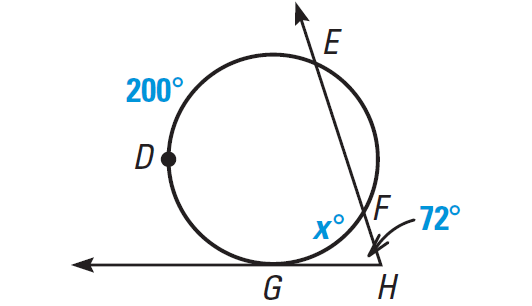
Solution :

Using Theorem 2, we have

m∠ GHF  =  1/2 ⋅ (m∠EDG - m∠GF)

72°  =  1/2 ⋅ (200° - x°)

Multiply each side by 2. 

144  =  200 - x

Solve for x.

x  =  56

Example 6 :

Find the value of x in the diagram shown below. 

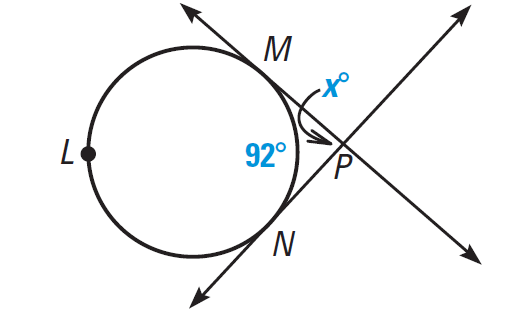
Solution :

Arcs MN and MLN make a whole circle. So, we have

m∠arc MLN + m∠MN  =  360°

Plug m∠MN  =  92°.

m∠arc MLN + 92°  =  360°

Subtract 92° from each side. 

m∠arc MLN  =  360° - 92°

m∠arc MLN  =  268°

Using Theorem 2, we have

x°  =  1/2 ⋅ (m∠MLN - m∠MN)

x°  =  1/2 ⋅ (268° - 92°)

x  =  1/2 ⋅ (176)

x  =  88

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.