ANGLE RELATIONSHIPS IN PARALLEL LINES AND TRIANGLES

Angle Pairs Formed by a Transversal

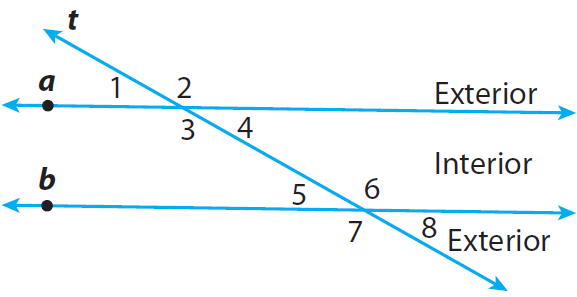
Corresponding Angles :

Angles lie on the same side of the transversal t, on the same side of lines a and b.

Example : ∠ 1 and ∠ 5.

Alternate Interior Angles :

Angles are nonadjacent angles that lie on opposite sides of the transversal t, between lines a and b.

Example : ∠ 3 and ∠ 6.

Alternate Exterior Angles :

Angles lie on opposite sides of the transversal t, outside lines a and b. 

Example : ∠ 1 and ∠ 8.

Same-Side Interior Angles :

Angles lie on the same side of the transversal t, between lines a and b.

Example : ∠ 3 and ∠ 5.

Angle Relationships in Triangles

In this section, we are going to see the angle relationships in triangles through the following steps.

Step 1 :

Draw a triangle and cut it out. Label the angles A, B, and C.

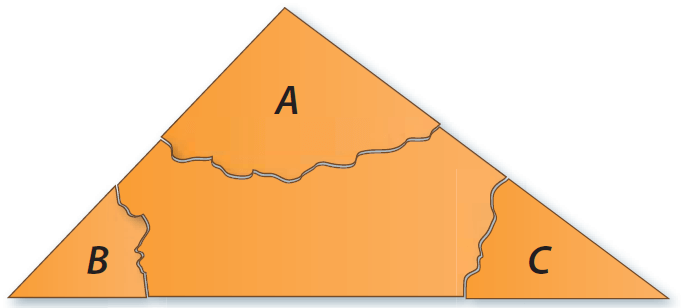
Step 2 :

Tear off each “corner” of the triangle. Each corner includes the vertex of one angle of the triangle.

Step 3 :

Arrange the vertices of the triangle around a point so that none of your corners overlap and there are no gaps between them.

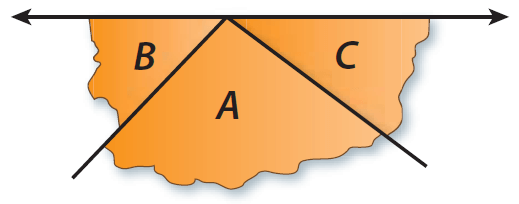
Step 4 :

What do you notice about how the angles fit together around a point ?

The angles form a straight angle.

Step 5 :

What do you notice about how the angles fit together around a point ?

180°

Step 6 :

Describe the relationship among the measures of the angles of triangle ABC ?

The sum of the angle measures is 180°.

Step 7 :

What does the triangle sum theorem state ?

The triangle sum theorem states that for triangle ABC,

m∠A + m∠B + m∠C = 180°

Exterior Angle Theorem in Triangles

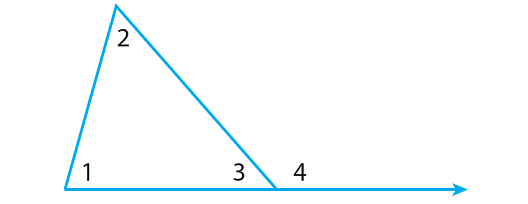
The theorem states that the measure of an exterior  angle is equal to the sum of its  remote interior angles.

That is, 

m∠1 + m∠2 = m∠4

Solved Problems

Problem 1 :

In the figure given below,  let the lines l₁ and l₂ be parallel and m is transversal. If ∠F = 65°, find the measure of each of the remaining angles.

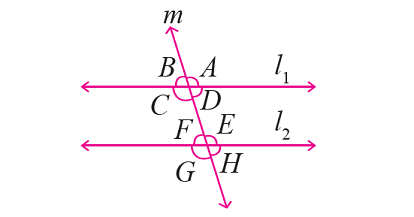
Solution :

From the given figure,

∠F and ∠H are vertically opposite angles and they are equal.

Then,

∠H = ∠F ----> ∠H = 65°

∠H and ∠D are corresponding angles and they are equal. 

Then,

∠D = ∠H ----> ∠D = 65°

∠D and ∠B are vertically opposite angles and they are equal.

Then,

∠B = ∠D ----> ∠B = 65°

∠F and ∠E are together form a straight angle.

Then, we have

∠F + ∠E = 180°

Substitute ∠F = 65°.

∠F + ∠E = 180°

65° + ∠E = 180°

∠E = 115°

∠E and ∠G are vertically opposite angles and they are equal.

Then,

∠G = ∠E ----> ∠G = 115°

∠G and ∠C are corresponding angles and they are equal.

Then,

∠C = ∠G ----> ∠C = 115°

∠C and ∠A are vertically opposite angles and they are equal.

Then,

∠A = ∠C ----> ∠A = 115°

Therefore,

∠A = ∠C = ∠E = ∠G = 115°

∠B = ∠D = ∠F = ∠H = 65°

Problem 2 :

In a triangle, if the second angle is 5° greater than the first angle and the third angle is 5° greater than second angle, find the three angles of the triangle.

Solution :

Let x be the first angle.

The second angle = x + 5.

The third angle = x + 5 + 5 = x + 10.

We know that, 

the sum of the three angles of a triangle = 180°

x + (x + 5) + (x + 10) = 180

3x + 15 = 180

3x = 165

x = 55

The first angle = 55°.

The second angle = 55 + 5 = 60°.

The third angle = 60 + 5 = 65°.

So, the three angles of a triangle are 55°, 60° and 65°.

Problem 3 :

Find m∠W and m∠X in the triangle given below.

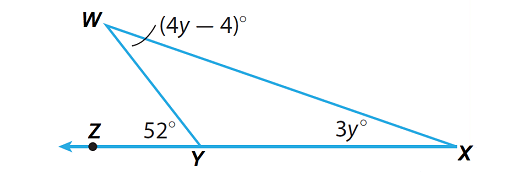
Solution :

Step 1 :

Write the Exterior Angle Theorem as it applies to this triangle.

m∠W + m∠X = m∠WYZ

Step 2 :

Substitute the given angle measures.

(4y - 4)° + 3y° = 52°

Step 3 :

Solve the equation for y.

(4y - 4)° + 3y° = 52°

4y - 4 + 3y = 52

Combine the like terms.

7y - 4 = 52

Add 4 to both sides.

7y - 4 + 4 = 52 + 4

Simplify.

7y = 56

Divide both sides by 7.

y = 8

Step 4 :

Use the value of y to find m∠W and m∠X.

So, m∠W = 28° and m∠X = 24°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.