ANGLE RELATIONSHIPS WORKSHEET

Problems 1-7 : Find the value of x in the diagram.

Problem 1 :

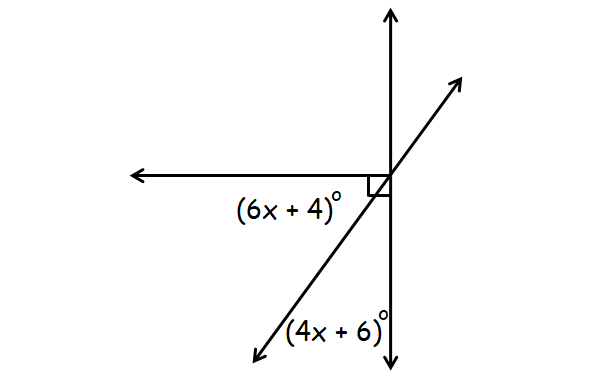
Problem 2 :

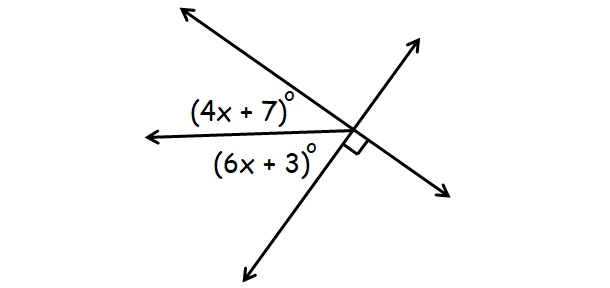
Problem 3 :

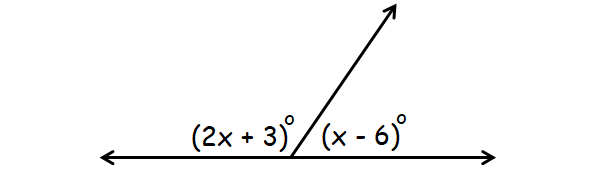
Problem 4 :

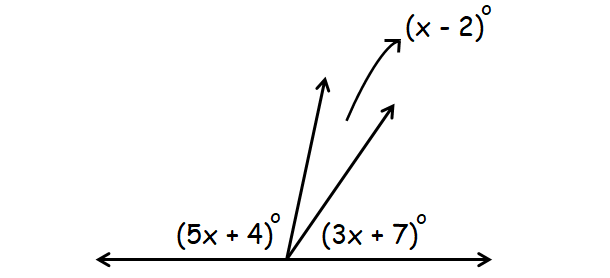
Problem 5 :

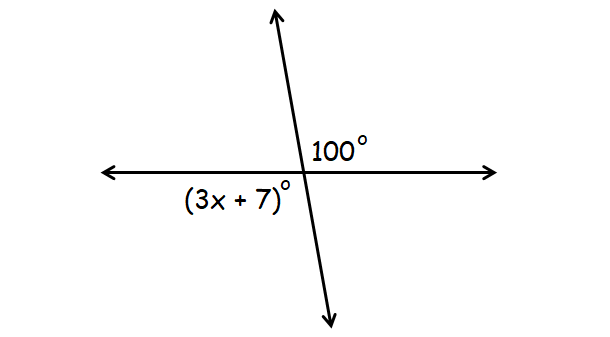
Problem 6 :

Problems 7-8 : In given the diagram, lines l₁ and l₂ are  parallel and t is a transversal. Find the value of x.

Problem 7 :

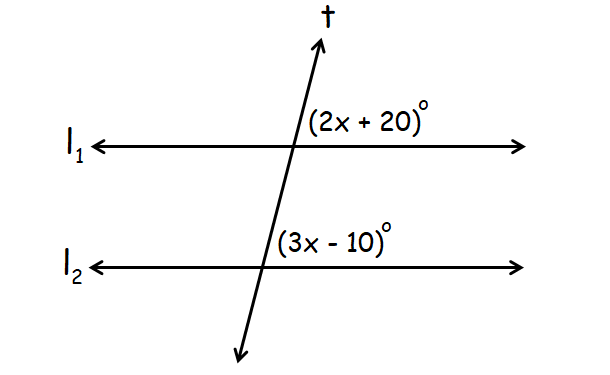
Problem 8 :

In the diagram given below,  l₁ lines l₂ are parallel and t is a transversal. Find the value of x.

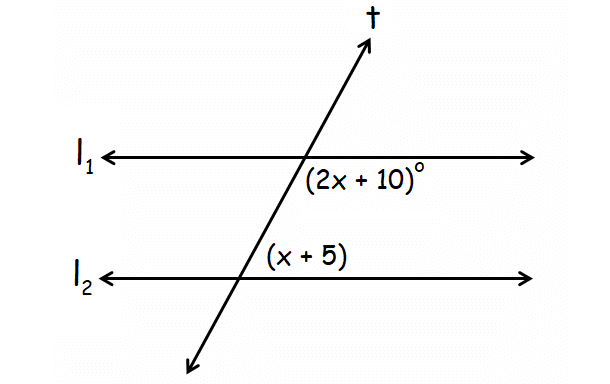
Problem 9 :

In the diagram given below,  a lines b are parallel and t is a transversal. Find the value of x.

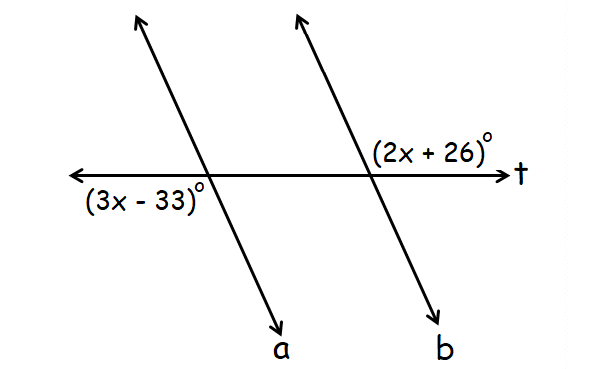
Problem 10 :

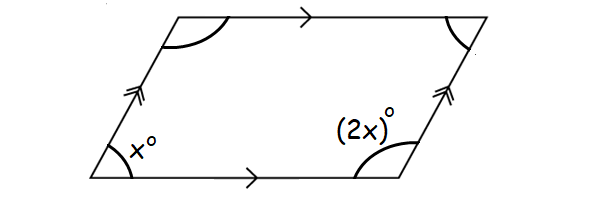
In the diagram given below, find the value of x.

Answers

1. Answer :

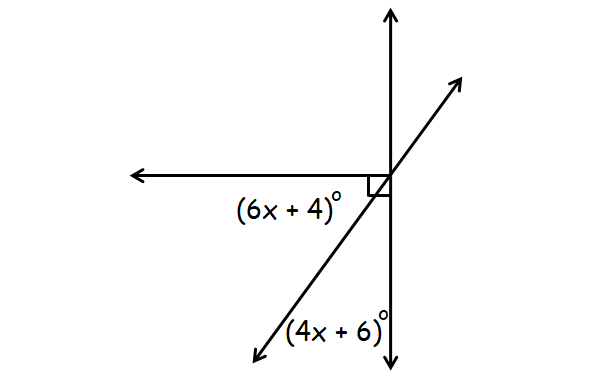
In the diagram above, (6x + 4)° and (4x + 6)° are complementary.  

(6x + 4)° + (4x + 6)° = 90°

6x + 4 + 4x + 6 = 90

10x + 10 = 90

10x = 80

x = 8

2. Answer :

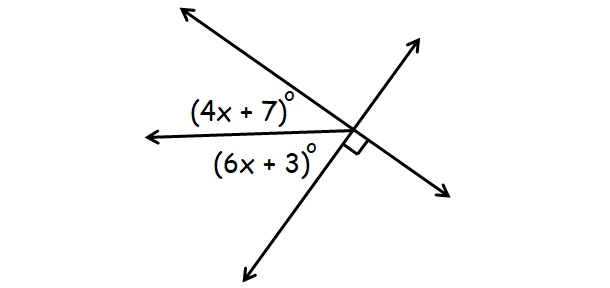
In the diagram above, (4x + 7)° and (6x + 3)° are complementary.  

(4x + 7)° + (6x + 3)° = 90°

4x + 7 + 6x + 3 = 90

10x + 10 = 90

10x = 80

x = 8

3. Answer :

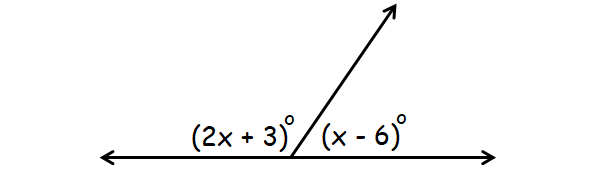
In the diagram above, (2x + 3)° and (x - 6)° are supplementary angles. 

(2x + 3)° + (x - 6)° = 180°

2x + 3 + x - 6 = 180

3x - 3 = 180

3x = 183

x = 61

4. Answer :

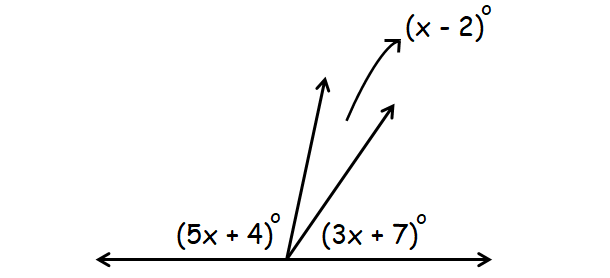
In the diagram above, (5x + 4)°, (x - 2)° and (3x + 7)° are supplementary angles. 

(5x + 4)° + (x - 2)° + (3x + 7)° = 180°

5x + 4 + x -2 + 3x + 7 = 180

9x + 9 = 180

9x = 171

x = 19

5. Answer :

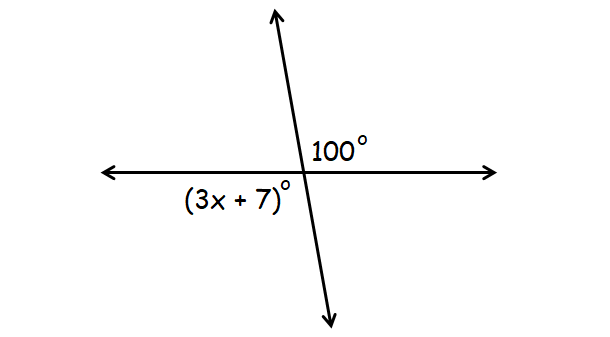
In the diagram above, (3x + 7)° and 100° are vertical angles.

(3x + 7)° = 100°

3x + 7 = 100

3x = 93

x = 31

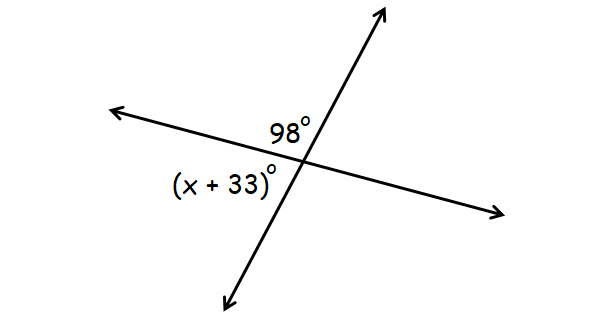
6. Answer :

In the diagram above, (x + 33)° and 98° form a linear pair.

(x + 33)° + 98° = 180°

x + 33 + 98 = 180

x + 131 = 180

x = 49

7. Answer :

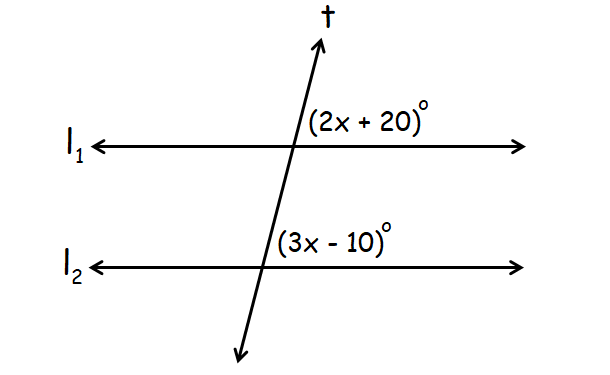
In the above diagram, (2x + 20)° and (3x - 10)° are corresponding angles. 

When two parallel lines are cut by a transversal, corresponding angles are congruent. 

(2x + 20)° = (3x - 10)°

2x + 20 = 3x - 10

30 = x

8. Answer :

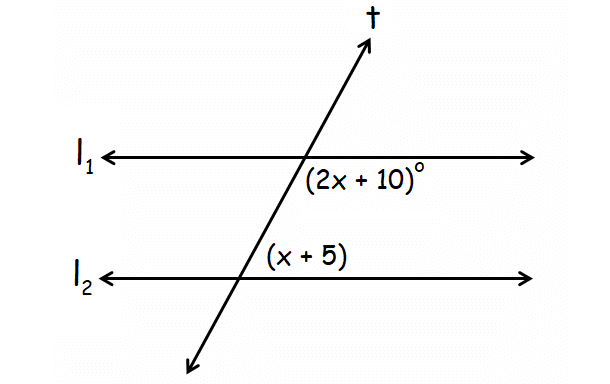
In the above diagram, (2x + 10)° and (x + 5)° are consecutive interior angles. 

When two parallel lines are cut by a transversal, consecutive interior angles are supplementary. 

(2x + 10)° + (x + 5)° = 180°

2x + 10 + x + 5 = 180

3x + 15 = 180

3x = 165

x = 55

9. Answer :

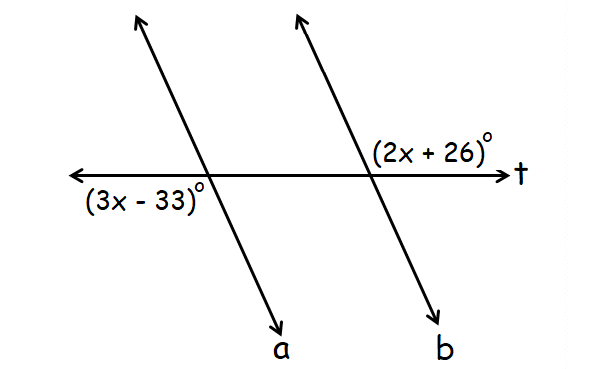
In the diagram diagram, (2x + 26)° and (3x - 33)° are alternate interior angles. 

When two parallel lines are cut by a transversal, alternate interior angles are congruent.

(2x + 26)° = (3x - 33)°

2x + 26 = 3x - 33

59 = x

10. Answer :

In the diagram diagram, it is clear that AB||CD and AD||BC.

So ABCD is a parallelogram. 

In a parallelogram, two consecutive angles are always supplementary. 

x° + (2x)° = 180°

x + 2x = 180

3x = 180

x = 60

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.