ANGLE RELATIONSHIPS

Two or more angles can be related, if certain conditions are met. Here, we will learn different types of angle relationships. 

(i)  Congruent Angles

(ii)  Vertical Angles

(iii)  Complementary Angles

(iv)  Supplementary Angles

(v)  Adjacent Angles

(vi)  Adjacent Angles in Parallelogram

(vii)  Linear Pair

(viii)  Corresponding Angles

(ix)  Alternate Interior Angles

(x)  Alternate Exterior Angles

(xi)  Consecutive Interior Angles

(xii)  Consecutive Exterior Angles 

Let us see the above different types of angle relationships in detail. 

(i) Congruent Angles : 

Congruent angles are angles that have the same measure.

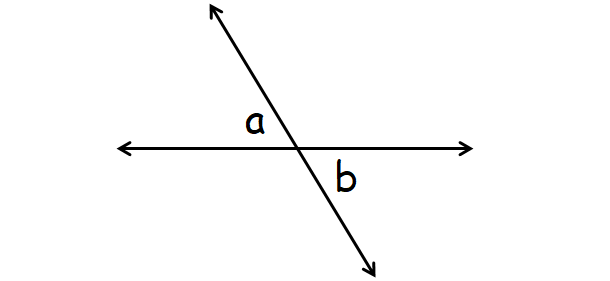
(ii) Vertical Angles : 

Vertical angles have a common vertex, but they are never adjacent angles. And also, vertical angles are always congruent.

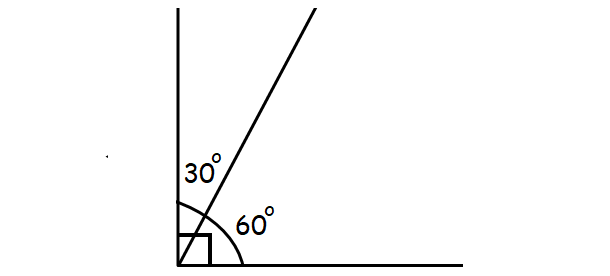
(iii) Complementary Angles : 

If the sum of two angles is 90⁰, then those two angles are called as complementary angles.

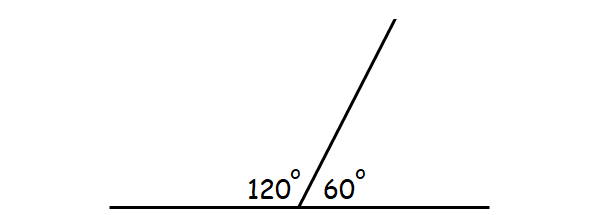
(iv) Supplementary Angles : 

If the sum of two angles is 180°, then those two angles are called as supplementary angles.

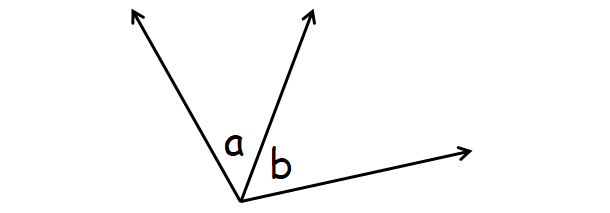
(v) Adjacent Angles : 

Adjacent angles are two angles that have a common vertex and a common side. 

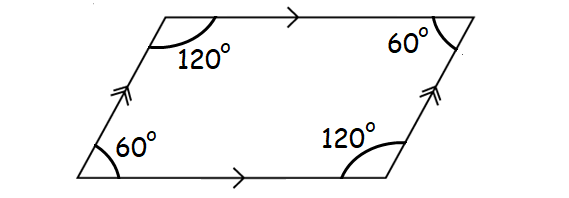
(vi) Consecutive Angles in Parallelogram : 

Any two consecutive angles of a parallelogram are supplementary. 

(vii) Linear Pair : 

A linear pair is a pair of adjacent angles formed when two lines intersect.

The two angles of a linear pair are always supplementary, which means their measures add up to 180°.

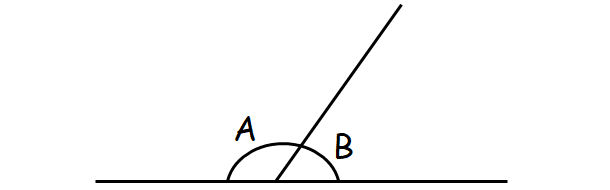
In the figure above A and B are linear pair. 

A + B = 180°

To know about Corresponding Angles, Alternate Interior Angles, Alternate Exterior Angles, Consecutive Interior Angles and Consecutive Exterior Angles in detail,

please click here

Solved Questions

Questions 1-7 : Find the value of x in the diagram.

Question 1 :

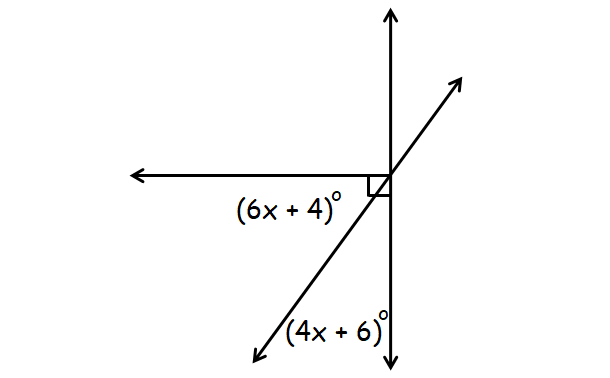
Answer :

In the diagram above, (6x + 4)° and (4x + 6)° are complementary.  

(6x + 4)° + (4x + 6)° = 90°

6x + 4 + 4x + 6 = 90

10x + 10 = 90

10x = 80

x = 8

Question 2 :

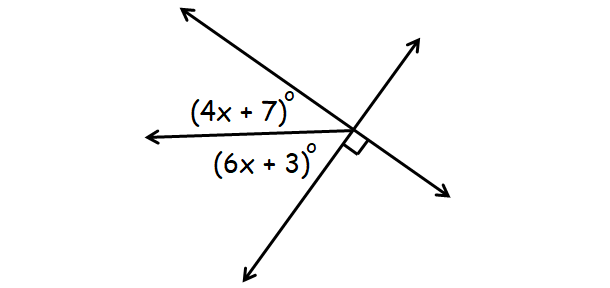
Answer :

In the diagram above, (4x + 7)° and (6x + 3)° are complementary.  

(4x + 7)° + (6x + 3)° = 90°

4x + 7 + 6x + 3 = 90

10x + 10 = 90

10x = 80

x = 8

Question 3 :

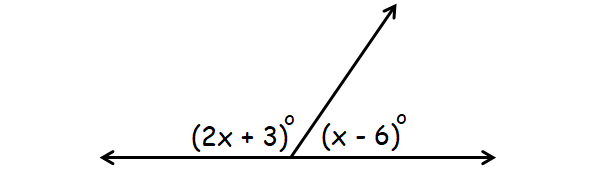
Answer :

In the diagram above, (2x + 3)° and (x - 6)° are supplementary angles. 

(2x + 3)° + (x - 6)° = 180°

2x + 3 + x - 6 = 180

3x - 3 = 180

3x = 183

x = 61

Question 4 :

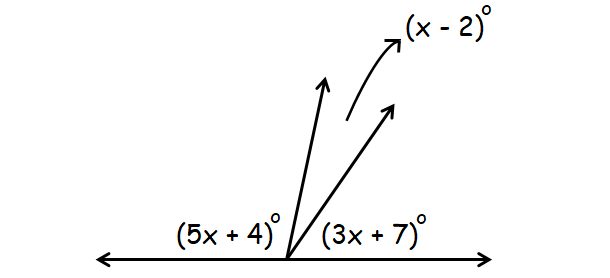
Answer :

In the diagram above, (5x + 4)°, (x - 2)° and (3x + 7)° are supplementary angles. 

(5x + 4)° + (x - 2)° + (3x + 7)° = 180°

5x + 4 + x -2 + 3x + 7 = 180

9x + 9 = 180

9x = 171

x = 19

Question 5 :

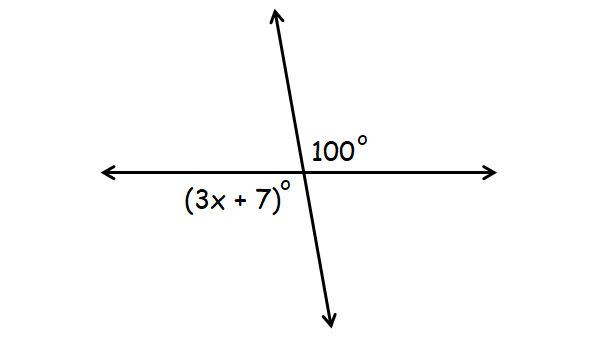
Answer :

In the diagram above, (3x + 7)° and 100° are vertical angles.

(3x + 7)° = 100°

3x + 7 = 100

3x = 93

x = 31

Question 6 :

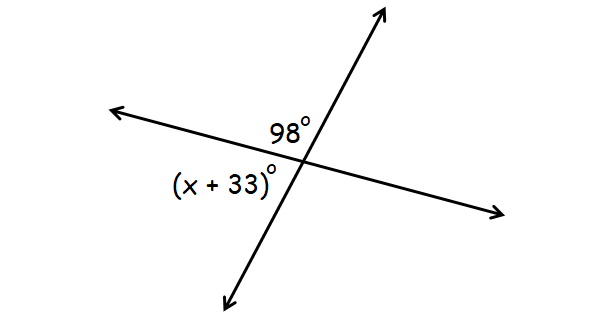
Answer :

In the diagram above, (x + 33)° and 98° form a linear pair.

(x + 33)° + 98° = 180°

x + 33 + 98 = 180

x + 131 = 180

x = 49

Question 7 :

In the diagram given below,  l₁ lines l₂ are parallel and t is a transversal. Find the value of x.

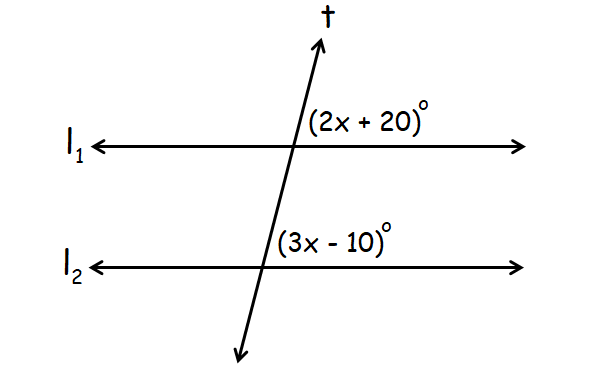
Answer :

In the above diagram, (2x + 20)° and (3x - 10)° are corresponding angles. 

When two parallel lines are cut by a transversal, corresponding angles are congruent. 

(2x + 20)° = (3x - 10)°

2x + 20 = 3x - 10

30 = x

Question 8 :

In the diagram given below, l₁ lines l₂ are parallel and t is a transversal. Find the value of x.

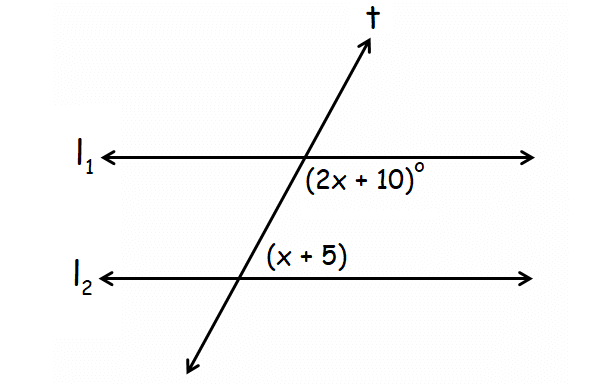
Answer :

In the above diagram, (2x + 10)° and (x + 5)° are consecutive interior angles. 

When two parallel lines are cut by a transversal, consecutive interior angles are supplementary. 

(2x + 10)° + (x + 5)° = 180°

2x + 10 + x + 5 = 180

3x + 15 = 180

3x = 165

x = 55

Question 9 :

In the diagram given below,  lines a and b are parallel and t is a transversal. Find the value of x.

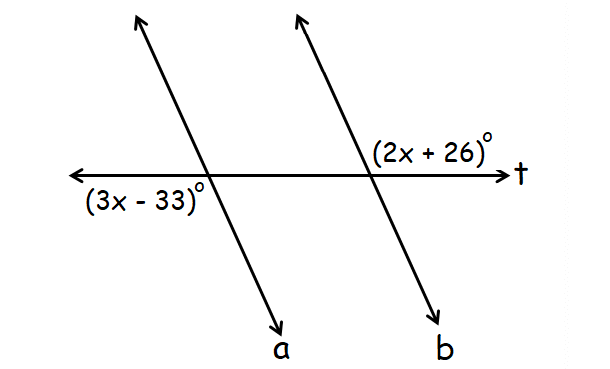
Answer :

In the diagram diagram, (2x + 26)° and (3x - 33)° are alternate interior angles. 

When two parallel lines are cut by a transversal, alternate interior angles are congruent.

(2x + 26)° = (3x - 33)°

2x + 26 = 3x - 33

59 = x

Question 10 :

In the diagram shown below, find the value of x.

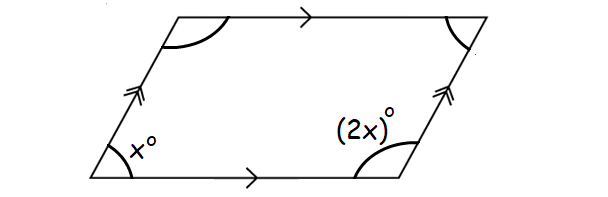
Answer :

In the diagram diagram, it is clear that AB||CD and AD||BC.

So ABCD is a parallelogram. 

In a parallelogram, two consecutive angles are always supplementary. 

x° + (2x)° = 180°

x + 2x = 180

3x = 180

x = 60

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.