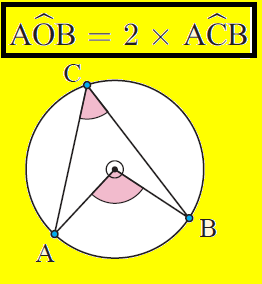
ANGLE SUBTENDED AT THE CENTER OF A CIRCLE

The angle at the center of a circle is twice the angle on the circle subtended by the same arc

Find, giving reasons, the values of the pronumerals in the following:

Example 1 :

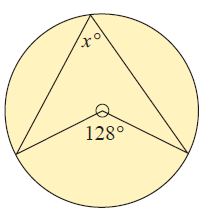
Solution :

<AOB  =  128 (Given)

<AOB  =  2<ABC

Angle subtended at the center is twice the angle subtended by the same arc.

2x  =  128

x  =  128/2

x  =  64

Example 2 :

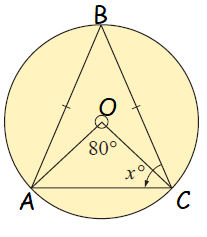
Solution :

<AOC  =  2<ABC

2<ABC  =  80

<ABC  =  40

In triangle ABC,

AB  =  BC

So, <BAC  =  <BCA  =  x

<ABC + <BCA + <BAC  =  180

40+x+x  =  180

2x  =  180-40

2x  =  140

x  =  70

Example 3 :

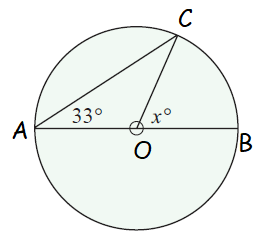
Solution :

<COB  =  x

OA  =  OB  =  radius

<OAC  =  <OCA  =  33

In triangle AOC

<OAC + <OCA + <AOC  =  180

33+33+<AOC  =  180

<AOC  =  180-66

<AOC  =  114

<AOC + <COB  =  180

114+x  =  180

x  =  180-114

x  =  66

Example 4 :

Solution :

<AOD  =  88

2<ABC  =  88

<ABC  =  44

In triangle ABC,

<CBA + <BAC + <ACB  =  180

44+50+<ACB  =  180

94+<ABC  =  180

<ABC  =  180-94

<ABC  =  86

<BCA + <ACD  =  180

86+x  =  180

x  =  180-86

x  =  94

Example 5 :

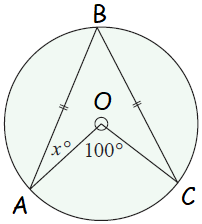
Solution :

<AOC  =  100

2<ABC  =  <AOB

2<ABC  =  100

<ABC  =  50

ABCO is a quadrilateral.

<OAB + <ABC + <BCO + <AOC  =  360

x + 50 + x + 260  =  360

2x + 310  =  360

2x  =  360-310

2x  =  50

x  =  25

Example 6 :

Solution :

<OAB  =  45, <OBA  =  45, <AOB  =  90

<ADB  =  90

<AOB  =  90 (2 times of <ADB because angle at the center)

<ADB  =  90/2

<ADB  =  45

Example 7 :

.In figure, if ∠OAB = 40°, then what is the measure of ∠ACB?

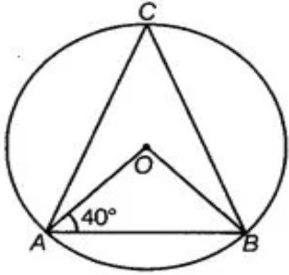
Solution :

In triangle AOB,

<OAB = 40 degree

<OBA = 40 degree

In triangle sum of the interior angles of triangle is 180 degree.

<OAB + <OBA + <AOB = 180

40 + 40 + <AOB = 180

<AOB = 180 - 80

<AOB = 100

<AOB = 2<ACB

100 = 2<ACB

<ACB = 100/2

= 50°

Example 8 :

.In figure, if ∠ ABC = 20°, then ∠AOC is equal to

a)20°           (b) 40°    (c) 60°      (d)10°

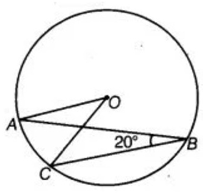
Solution :

Angle at the center of the circle is 2 times angle at the circumference of the circle.

<AOC = 2<ABC

<AOC = 2(20)

<AOC = 40°

Example 9 :

In Figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.

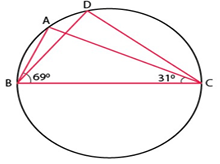
Solution :

In triangle ABC,

∠ABC + ∠ACB + ∠BAC = 180

Given that, ∠ABC = 69°, ∠ACB = 31°

69 + 31 + ∠BAC = 180

100 + ∠BAC = 180

∠BAC = 180 - 100

∠BAC = 80

Example 10 :

In Figure, ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.

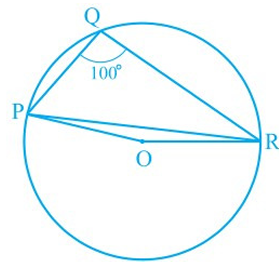
Solution :

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

A quadrilateral ABCD is called cyclic if all the four vertices of it lie on a circle and the sum of either pair of opposite angles of a cyclic quadrilateral is 180°.

Mark any point on the major arc side (opposite side to point Q) as S

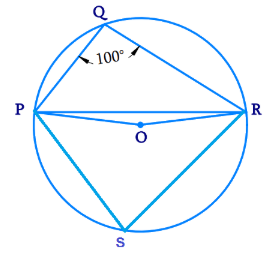
Since all points P, Q, R, S lie on the circle, PQRS becomes a cyclic quadrilateral.

We know that the sum of either pair of opposite angles of a cyclic quadrilateral is 180°.

Therefore,

∠PQR + ∠PSR = 180°

100° + ∠PSR = 180°

∠PSR = 180° - 100° = 80°

We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

Therefore,

∠POR = 2∠PSR

= 2 × 80°

= 160°

Example 11 :

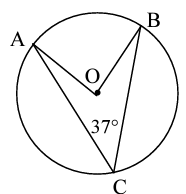
∠ACB is an inscribed angle made by arc ______. The central angle made by the same arc is __________. Therefore, the measurement of ∠AOB is ______°.

Solution :

∠ACB is an inscribed angle made by arc AB. The central angle made by the same arc is ∠ACB. Therefore, the measurement of ∠AOB is 2∠ACB°.

Example 12 :

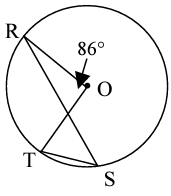
∠ROT is a central angle made by arc ______. An inscribed angle made by the same arc is __________. Therefore, the measure of ∠RST is ______°.

Solution :

∠ROT is a central angle made by arc RT. An inscribed angle made by the same arc is ∠RST. Therefore, the measure of ∠RST is equal to half of ∠ROT°.

∠RST = 1/2 of ∠ROT

= (1/2) x 86

= 43

Example 13 :

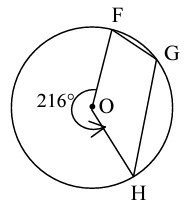
Reflex ∠FOH is the central angle made by major arc ______. An inscribed angle made by the same arc is __________. Therefore, the measure of ∠FGH is _____°.

Solution :

Reflex ∠FOH = 360 - 216

Inscribed angle = 144

Reflex ∠FOH is the central angle made by major arc FH. An inscribed angle made by the same arc is ∠FOH. Therefore, the measure of ∠FGH is 2∠FOH°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.