ANGLE SUBTENDED BY AN ARC AT THE CENTER OF THE CIRCLE
The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
 |
 |
 |
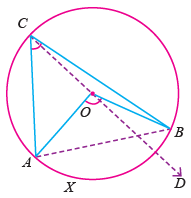
O is the centre of the circle. AXB is the arc. AOB is the angle subtended by the arc AXB at the centre. <ACB is the angle subtended by the arc AXB at a point on the remaining part of the circle |
To prove : ∠AOB = 2∠ACB
Construction : Join CO and produce it to D
(i) OA = OC (Radii)
(ii) ∠OCA = ∠OAC
(angles opposite to equal sides are equal.)
(iii) In ΔAOC
∠<AOD = ∠OCA + ∠OAC
(Exterior angles of a triangle = Sum of the interior opposite angles)
(iv) ∠AOD = ∠OCA + ∠OCA
(substituting <OAC by <OCA)
(v) ∠AOD = 2∠OCA (by addition)
(vi) Similarly in triangle BOC
∠BOD = 2∠OCB
(vii) ∠AOD + ∠BOD = 2∠OCA + 2∠OCB
= 2(∠OCA + ∠OCB)
(∠AOD + ∠BOD = ∠AOB and ∠OCA + ∠OCB = ∠ACB)
(viii) ∠AOB = 2∠ACB
Example 1 :
Find the value of x in the following figure.
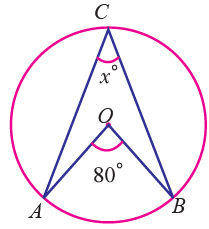
Solution :
Using the theorem the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
(i) ∠AOB = 2∠ACB
∠ACB = (1/2)∠AOB
= (1/2) ⋅ 80°
= 40°
Example 2 :
Find the value of x in the following figure.
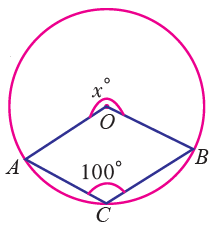
Solution :
reflex ∠AOB = 2∠ACB
x = 2 ⋅ 100° = 200°
Example 3 :
Find the value of x in the following figure.
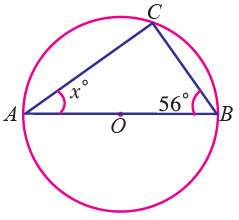
∠ABC + ∠BCA + ∠CAB = 180°
56° + 90° + ∠CAB = 180°
(a ∠BCA = angle on a semicircle = 90°)
∠CAB = 180° - 146°
x = 34°
Example 4 :
Find the value of x in the following figure.
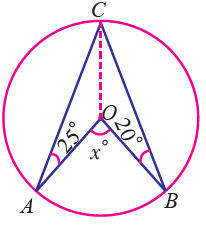
OA = OB = OC ( radius )
∠OCA = ∠OAC = 25°
∠OBC = ∠OCB = 20°
∠ACB = ∠OCA + ∠OCB
= 25° + 20° = 45°
AOB = 2∠ACB
x = 2(45°)
= 90°
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

