ANGLE SUBTENDED BY AN ARC AT THE CENTER WORKSHEET
|
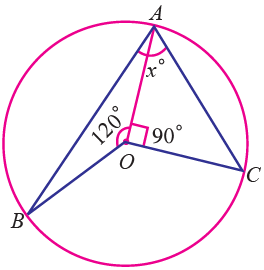
(1) Find the value of x in the following figure. |
 |
|
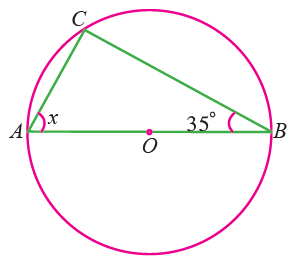
(2) Find the value of x in the following figure. |
 |
|
(3) Find the value of x in the following figure. |
 |
|
(4) Find the value of x in the following figure. |
 |
|
(5) Find the value of x in the following figure. |
 |
|
(6) Find the value of x in the following figure. |
 |
|
(7) Find the value of x in the following figure. |
 |
|
(8) Find the value of x in the following figure. |
 |
|
(9) Find the value of x in the following figure. |
 |
|
(10) Find the value of x in the following figure. |
 |

Detailed Answer Key
Question 1 :
Find the value of x in the following figure.

Solution :
According to the theorem,
∠BOC = 2∠BAC -----(1)
∠BOC = 2x
∠BOC + ∠BOA + ∠AOC = 360°
∠BOC + 120 + 90 = 360
∠BOC + 210 = 360
∠BOC = 360 - 210
∠BOC = 150°
From this we may find the value of ∠BAC. That is x
From (1)
∠BOC = 2∠BAC
150 = 2∠BAC
∠BAC = 150/2
= 75°
So, the value of x is 75.
Question 2 :
Find the value of x in the following figure.

Solution :
The angle in a semicircle is right angle.
∠ACB = 90°
Sum of interior angels in a triangle is 180°.
∠CAB + ∠ACB + ∠ABC = 180°
x + 90 + 35 = 180
x + 125 = 180
x = 180 - 125
x = 55
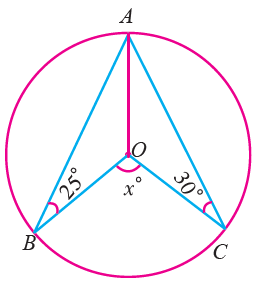
Question 3 :
Find the value of x in the following figure.

OA = OB = OC ( radius )
∠OCA = ∠OAC = 30°
∠OBA = ∠OAB = 25°
∠BOC = 2∠BAC
∠BAC = ∠BAO + ∠OAC
= 25 + 30
= 55°
∠BOC = 2(55) = 110°
So, the value of x is 110.
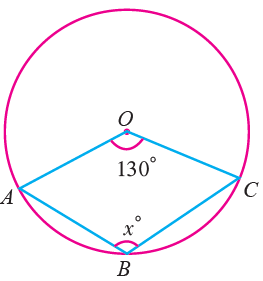
Question 4 :
Find the value of x in the following figure.

Solution :
reflex ∠AOC = 360 - 130 = 230°
2∠ABC = reflex of ∠AOC
Reflex of ∠AOC = 2x
x = Reflex of ∠AOC / 2
= 230/2
= 115°
So, the value of x is 115.
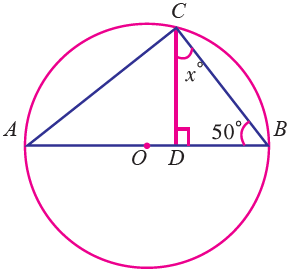
Question 5 :
Find the value of x in the following figure.

Solution :
In triangle DBC,
∠DBC + ∠DCB + ∠CDB = 180°
∠CDB = 90°
50 + x + 90 = 180
140 + x = 180°
x = 180 - 140
x = 40
So, the value of x is 40.
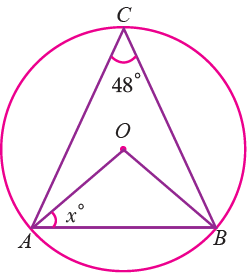
Question 6 :
Find the value of x in the following figure.

∠AOB = 2∠ACB
∠AOB = 2(48) = 96
In triangle AOB,
∠OAB + ∠ABO + ∠BOA = 180
OA = OB = OC = Radius
∠OAB = ∠OBA = x
x + x + 96 = 180
2x + 96 = 180
2x = 180 - 96
2x = 84
x = 84/2
x = 42
So, the value of x is 42.
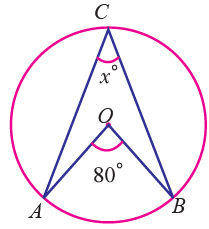
Question 7 :
Find the value of x in the following figure.

Solution :
Using the theorem the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
∠ACB = (1/2)∠AOB
x° = (1/2) ⋅ 80°
x° = 40°
So, the value of x is 40.
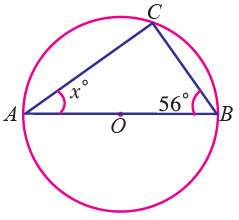
Question 8 :
Find the value of x in the following figure.

Solution :
reflex ∠OB = 2∠ACB
x = 2 ⋅ 100° = 200°
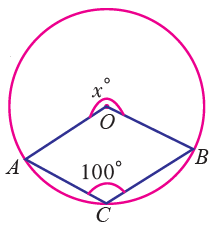
Question 9 :
Find the value of x in the following figure.

∠ABC + ∠BCA + ∠CAB = 180°
56° + 90° + ∠CAB = 180°
(∠BCA = angle on a semicircle = 90°)
∠CAB = 180° - 146°
x° = 34°
So, the value of x is 34.
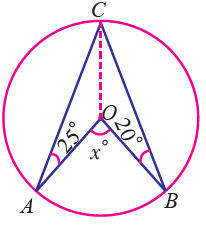
Question 10 :
Find the value of x in the following figure.

OA = OB = OC ( radius )
∠OCA = ∠OAC = 25°
∠OBC = ∠OCB = 20°
∠ACB = ∠OCA + ∠OCB
= 25° + 20° = 45°
∠AOB = 2∠ACB
x° = 2(45°)
x° = 90°
So, the value of x is 90.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)