ANGLE SUBTENDED BY AN ARC AT THE CENTER OF THE CIRCLE

The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

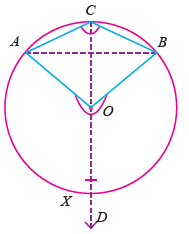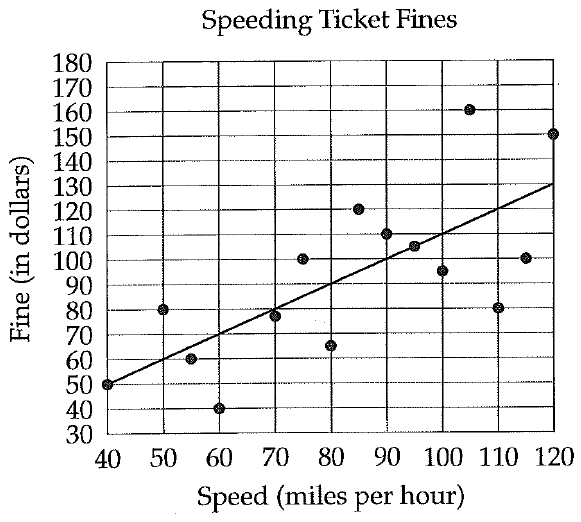
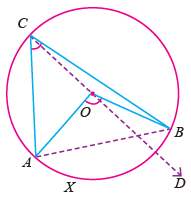
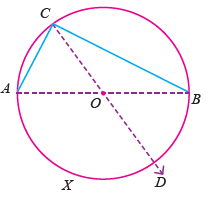
	O is the centre of the circle. AXB is the arc. AOB is the angle  subtended by the arc AXB at the centre. <ACB is the angle subtended by the arc AXB at a point on the remaining part of the circle

To prove : ∠AOB  =  2∠ACB

Construction : Join CO and produce it to D

(i) OA  =  OC     (Radii)

(ii) ∠OCA  =  ∠OAC 

(angles opposite to equal sides are equal.)

(iii) In ΔAOC 

∠<AOD  =  ∠OCA + ∠OAC

(Exterior angles of a triangle  =  Sum of the interior opposite angles)

(iv) ∠AOD  =  ∠OCA + ∠OCA

(substituting <OAC by <OCA)

(v) ∠AOD  =  2∠OCA (by addition)

(vi) Similarly in triangle BOC

∠BOD  =  2∠OCB

(vii) ∠AOD + ∠BOD  =  2∠OCA + 2∠OCB

=  2(∠OCA + ∠OCB) 

(∠AOD + ∠BOD  =  ∠AOB and ∠OCA + ∠OCB  =  ∠ACB)

(viii) ∠AOB  =  2∠ACB

Example 1 :

Find the value of x in the following figure.

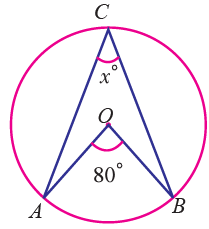
Solution :

Using the theorem the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

(i) ∠AOB  =  2∠ACB

∠ACB  =  (1/2)∠AOB

  =  (1/2) ⋅ 80°

 =  40°

Example 2 :

Find the value of x in the following figure.

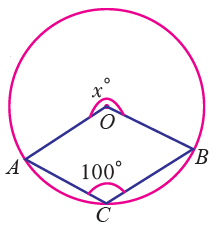
Solution :

reflex ∠AOB  =  2∠ACB

x = 2 ⋅ 100°  =  200°

Example 3 :

Find the value of x in the following figure.

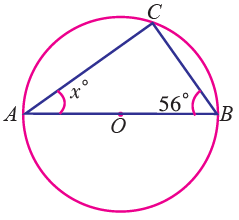
∠ABC + ∠BCA + ∠CAB  =  180°

56° + 90° + ∠CAB  =  180°

(a ∠BCA = angle on a semicircle  =  90°)

∠CAB  =  180° -  146°

x  =  34°

Example 4 :

Find the value of x in the following figure.

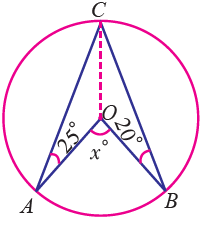
OA = OB = OC ( radius )

∠OCA  =  ∠OAC  =  25°

∠OBC  =  ∠OCB = 20°

∠ACB  =  ∠OCA + ∠OCB

= 25° + 20°  =  45°

AOB  =  2∠ACB

x  =  2(45°) 

=  90°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.