ANGLE SUBTENDED BY AN ARC AT THE CENTRE PRACTICE

Solved Examples

Example 1 :

Find the value of x in the following figure.

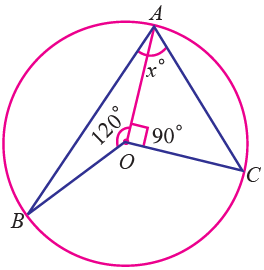
Solution :

According to the theorem,

∠BOC  =  2∠BAC -----(1)

∠BOC  =  2x

∠BOC  + ∠BOA + ∠AOC   =  360°

∠BOC  + 120 + 90  =  360

∠BOC  + 210  =  360

∠BOC   =  360 - 210

∠BOC   =  150°

From this we may find the value of ∠BAC. That is x.

From (1)

∠BOC  =  2∠BAC 

150  =  2∠BAC 

∠BAC  =  150/2

=  75°

So, the value of x is 75°.

Example 2 :

Find the value of x in the following figure.

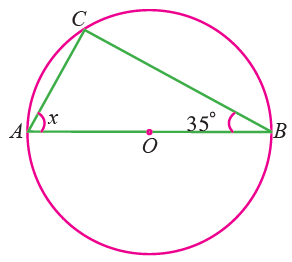
Solution :

The angle in a semicircle is right angle.

∠ACB  =  90°

Sum of interior angels in a triangle is 180°.

∠CAB + ∠ACB + ∠ABC  =  180

x + 90 + 35  =  180

x + 125  =  180

x  =  180 - 125

x  =  55°

Example 3 :

Find the value of x in the following figure.

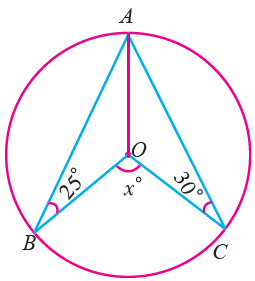
OA = OB = OC ( radius )

∠OCA  =  ∠OAC  =  30°

∠OBA  =  ∠OAB = 25°

∠BOC  =  2∠BAC

∠BAC  =  ∠BAO + ∠OAC

=  25 + 30

  =  55°

∠BOC  =  2(55)  =  110°

So, the value of x is 110°.

Example 4 :

Find the value of x in the following figure.

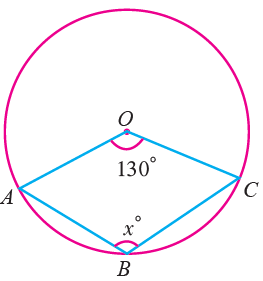
Solution :

reflex ∠AOC  =  360 - 130  =  230°

2∠ABC  =  reflex of ∠AOC

Reflex of ∠AOC  =  2x

x  =  Reflex of ∠AOC / 2

=  230/2

=  115°

So, the value of x is 115°.

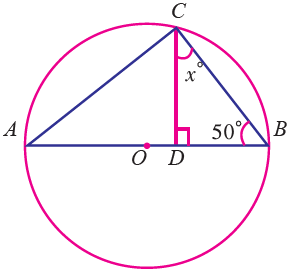
Example 5 :

Find the value of x in the following figure.

Solution :

In triangle DBC,

∠DBC + ∠DCB + ∠CDB  =  180°

∠CDB  =  90°

50 + x + 90  =  180°

140 + x  =  180°

x  =  180 - 140

x  =  40°

So, the value of x is 40°.

Example 6 :

Find the value of x in the following figure.

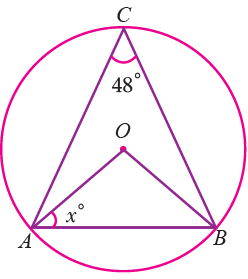
∠AOB  =  2∠ACB

∠AOB  =  2(48)  =  96

In triangle AOB,

∠OAB + ∠ABO + ∠BOA  =  180

OA  =  OB  =  OC  =  Radius

∠OAB  =  ∠OBA  =  x

x + x  + 96  =  180

2x + 96  =  180

2x  =  180 - 96

2x  =  84

x  =  84/2

x  =  42°

So, the value of x is 42°.

Example 7 :

Find the value of x in the following figure.

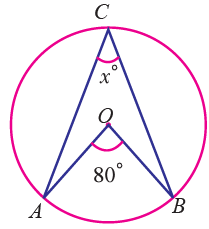
Solution :

Using the theorem the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.

(i) ∠AOB  =  2∠ACB

∠ACB  =  (1/2)∠AOB

  =  (1/2) ⋅ 80°

 =  40°

Example 8 :

Find the value of x in the following figure.

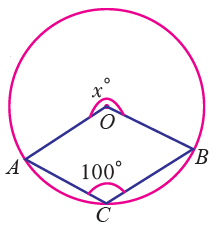
Solution :

reflex ∠AOB  =  2∠ACB

x  =  2 ⋅ 100°  =  200°

Example 9 :

Find the value of x in the following figure.

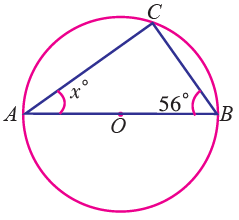
∠ABC + ∠BCA + ∠CAB  =  180°

56° + 90° + ∠CAB  =  180°

(∠BCA = angle on a semicircle  =  90°)

∠CAB  =  180° -  146°

x  =  34°

Example 10 :

Find the value of x in the following figure.

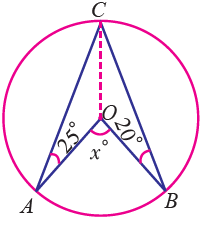
OA = OB = OC ( radius )

∠OCA  =  ∠OAC  =  25°

∠OBC  =  ∠OCB = 20°

∠ACB  =  ∠OCA + ∠OCB

= 25° + 20° =  45°

AOB  =  2∠ACB

x  =  2(45°) 

x  =  90°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.