ANGLES AND THEIR MEASURES WORKSHEET

Problem 1 :

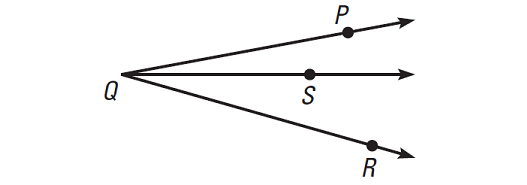
Name the angles in the figure given below.

Problem 2 :

Each eye of a horse wearing blinkers has an angle of vision that measures 100°. The angle of vision that is seen by both eyes measures 60°.

Find the angle of vision seen by the left eye alone.

Problem 3 :

Plot the points L (-4, 2), M(-1, -1), N (2, 2), Q(4, -1) and P(2, -4). Then, measure and classify the following angles as acute, right, obtuse or straight.

(i) m∠LMN

(ii) m∠LMP

(iii) m∠NMQ

(iv) m∠LMQ

Problem 4 :

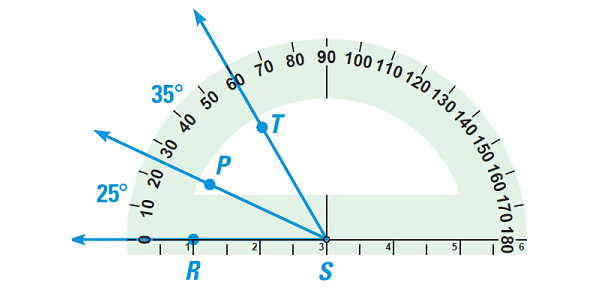
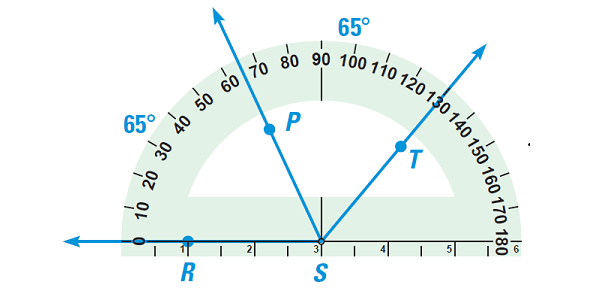
Use a protractor to draw two adjacent acute angles  ∠RSP and ∠PST so that ∠RST is

(a) Acute

(b) Obtuse

1. Answer :

There are three different angles.

∠PQS or ∠SQP

∠SQR or ∠RQS

∠PQR or ∠RQP

We should name any of the angles as ∠Q, because all three angles have Q as their vertex. The name ∠Q would not distinguish one angle from others.

2. Answer :

We can use the angle addition postulate. 

m∠2 + m∠3 = 100°   (The total for left eye is 100°)

m∠3 = 100° - m∠2   (Subtract m∠2 from each side)

m∠3 = 100° - 60°  (Substitute 60° for m∠2)

m∠3 = 40°   (Subtract)

Hence, the vision for the left eye alone measures is 40°.

3. Answer :

Plot the given points in xy coordinate plane.

We can use the protractor to measure and classify each angle as shown below.

Note : 

Two angles are adjacent angles, if they share a common vertex and side, but have no common interior points.   

4. Answer :

Solution (a) :

Solution (b) :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.