ANGLES FORMED BY PARALLEL LINES AND TRANSVERSAL

A transversal is a line that intersects two lines in the same plane at two different points.

In the diagram shown below, let the lines l₁ and l₂ be parallel. Because the line m cuts the lines l₁ and l₂, the line m is transversal. 

So, the two parallel lines l₁ and l₂ cut by the transversal m. 

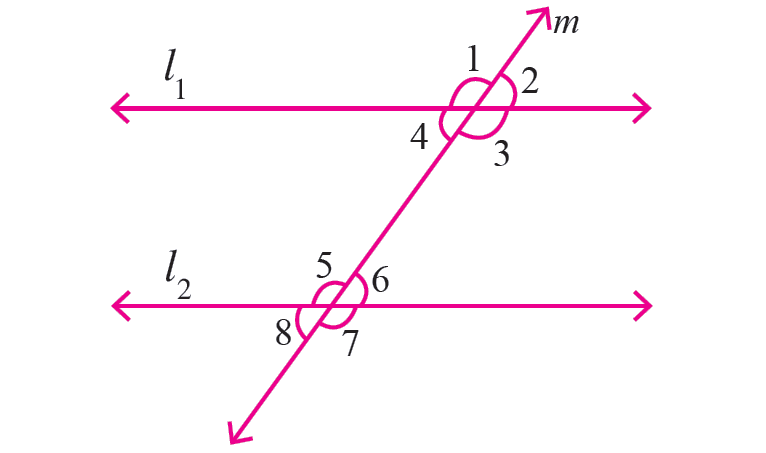
The angles formed by the two parallel lines l₁ and l₂ and the transversal min the above diagram will be as follows. 

Example 1 :

In the figure given below,  let the lines l₁ and l₂ be parallel and m is transversal. If m∠F = 65°, find the measure of each of the remaining angles.  

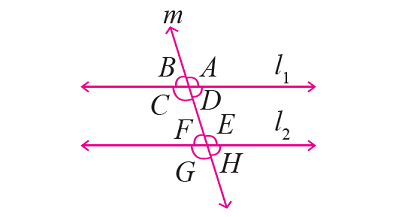
Solution :

In the figure above, ∠F and ∠H are vertically opposite angles and they are equal.

m∠H  =  m∠F

m∠H  =  65°

∠H and ∠D are corresponding angles and they are equal. 

m∠D  =  m∠H

m∠D  =  65°

∠D and ∠B are vertically opposite angles and they are equal. 

m∠B  =  m∠D

m∠B  =  65°

∠F and ∠E form a linear pair and they are supplementary. 

m∠F + m∠E  =  180°

Substitute m∠F  =  65°.

65° + m∠E  =  180°

m∠E  =  115°

∠E and ∠G are vertically opposite angles and they are equal. 

m∠G  =  m∠E

m∠G  =  115°

∠G and ∠C are corresponding angles and they are equal. 

m∠C  =  m∠G

m∠C  =  115°

∠C and ∠A are vertically opposite angles and they are equal. 

m∠A  =  m∠C

m∠A  =  115°

Therefore, 

m∠A  =  m∠C  =  m∠E  =  m∠G  =  115°

m∠B  =  m∠D  =  m∠F  =  m∠H  =  65°

Example 2 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of x.

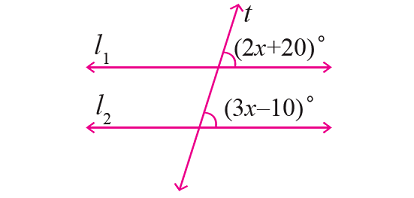
Solution :

In the figure above, (2x + 20)° and (3x - 10)° are corresponding angles and they are equal. 

(2x + 20)°  =  (3x - 10)°

2x + 20  =  3x - 10

30  =  x

Example 3 :

In the figure given below,  let the lines l₁ and l₂ be parallel and t is transversal. Find the value of x.

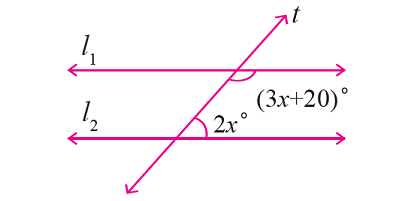
Solution :

In the figure above, (3x + 20)° and 2x° are consecutive interior angles and they are supplementary. 

(3x + 20)° + 2x°  =  180°

3x + 20 + 2x  =  180

5x + 20  =  180

5x  =  160

x  =  32

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.