ANGLES IN QUADRILATERALS WORKSHEET

Problem 1 :

Four angles of a quadrilateral are in the ratio 3 : 4 : 5 : 6. Find its angles.

Solution :

In a quadrilateral, the angles are in the ratio 3 : 4 : 5 : 6. Then the interior angles will be 3x, 4x, 5x and 6x.

Sum of interior angles of quadrilateral = 360

3x + 4x + 5x + 6x = 360

18x = 360

x = 360/18

x = 20

Applying the value of x in 3x, 4x, 5x and 6x, we get

3(20) ==> 60°

4(20) ==> 80°

5(20) ==> 100°

6(20) ==> 120°

So, the required angles are 60°, 80°, 100° and 120°.

Problem 2 :

The adjacent angels of a parallelogram are (3x - 4)° and (3x + 10)°. Find the angles of a parallelogram.

Solution :

In a parallelogram, opposite sides are parallel and equal. Adjacent angles will lie in between parallel sides.

(3x - 4) + (3x + 10) = 180

6x + 6 = 180

6x = 180 - 6

6x = 174

x = 29

Applying the value of x,

So, the required angels are 84° and 97°.

Problem 3 :

Three angles of a quadrilateral are in the ratio 4 : 6 : 3. If the fourth angle is 100°, find the three angles of a quadrilateral.

Solution :

The three angles are 4x, 6x and 3x

Sum of the interior angles = 360

4x + 6x + 3x + 100 = 360

13x = 360 - 100

13x = 260

x = 260/13

x = 20

Applying the value of x in 4x, 6x and 3x, we get

4(20) = 80°

6(20) = 120°

3(20) = 60°

So, the required angles are 80°, 120°, 60° and 100°

Problem 4 :

Find x + y + z + w

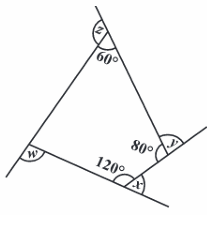
Solution :

By observing the figure, x and 120 are supplementary.

x + 120 = 180

x = 180 - 120

x = 60 ----(1)

y and 80 are supplementary.

80 + y = 180

y = 180 - 80

y = 100 ----(2)

z and 60 are supplementary.

z + 60 = 180

z = 180 - 60

z = 120 ----(3)

x + y + z + another interior angle = 360

60 + 100 + 120 + interior angle = 360

interior angle = 360 - 280

= 80

w = 180 - 80

w = 100 ----(4)

(1) + (2) + (3) + (4)

= 60 + 100 + 120 + 100

x + y + z + w = 380°

Problem 4 :

Find the angle x.

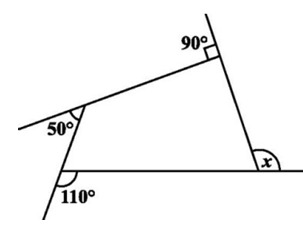
Solution :

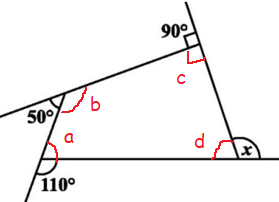
a = 180 - 110 ==> 70

50 + b = 180

b = 180 - 50 ==> 130

90 + c = 180

c = 180 - 90 ==> 90

d + x = 180 -----(1)

Sum of interior angles of a quadrilateral = 360

a + b + c + d = 360

70 + 130 + 90 + d = 360

290 + d = 360

d = 360 - 290

d = 70

By applying the value of d in (1), we get

70 + x = 180

x = 180 - 70

x = 110

Problem 5 :

Two adjacent angles of a parallelogram are as 2 : 3. Find the measure of each of its angles.

Solution :

Sum of adjacent angles of parallelogram = 180

Since the adjacent angles are in the ratio 2 : 3, let the angles be 2x and 3x.

2x + 3x = 180

5x = 180

x = 180/5

x = 36

2x = 2(36) ==> 72

3x = 3(36) ==> 108

So, the required angles are 72, 72, 108 and 108.

Problem 6 :

The angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle is 80°   . Find the obtuse angle.

Solution :

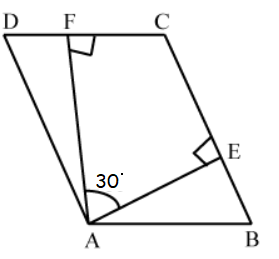
In the parallelogram above, 

AF and AE are altitudes of the parallelogram.

In the quadrilateral AEFC, 

<AFC = <AEC = 90

<FAE = 30

Here the obtuse angle is <FCE

30 + 90 + 90 + <FCE = 360

30 + 180 + <FCE = 360

210 + <FCE = 360

<FCE = 360 - 210

= 150

So, the required obtuse angle is 150 degree.

Problem 7 :

In a figure given below, ABCD is a parallelogram, what is the value of x ?

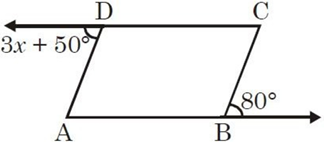
Solution :

Since ABCD is a parallelogram, AB and DC are parallel.

<ABC + 80 = 180

<ABC = 180 - 80

<ABC = 100

Then <ADC = 100 (opposite angles will be equal)

3x + 50 = 80

3x = 80 - 50

3x = 30

x = 10

So, the value of x is 10.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.