ANGLES IN STANDARD POSITION WORKSHEET

Draw the following angles in standard position. 

1)  -340°

2)  150°

3)  -185°

4)  300°

5)  220°

State the related angle for the following principal angles.

6)

7) 

8)

Find the measures of the following principal angles. 

9)

10)

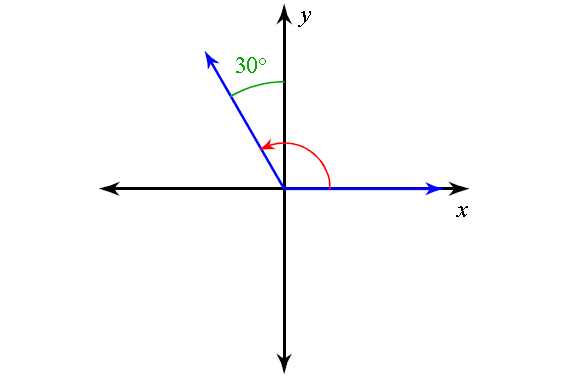
State the quadrant in which the terminal sides of the following angles lie. 

11)  300°

12)  40°

13)  -222°

14)  -30°

15)  103°

Answers

1. Answer :

-340°

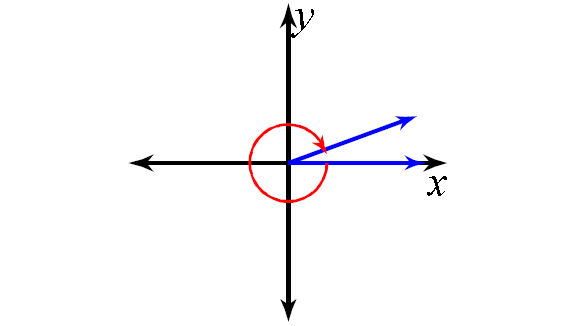
2. Answer :

150°

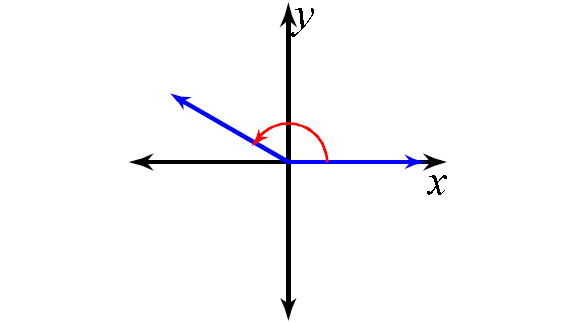
3. Answer :

-185°

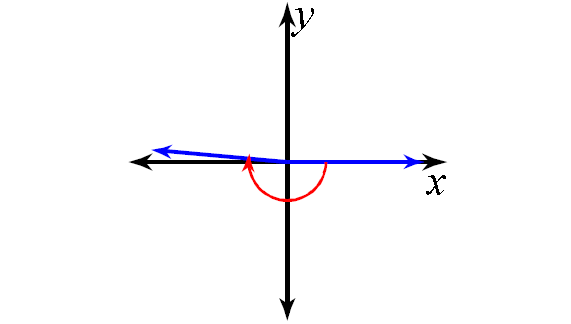
4. Answer :

300°

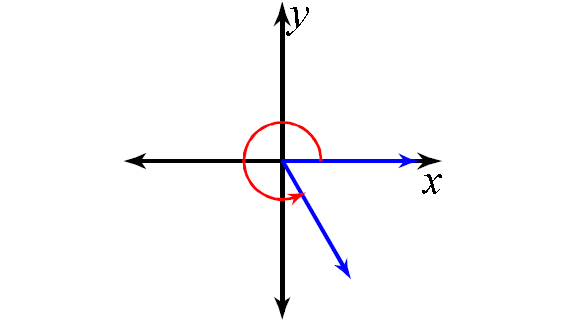
5. Answer :

220°

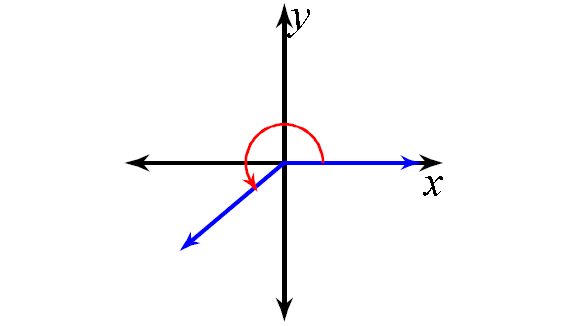
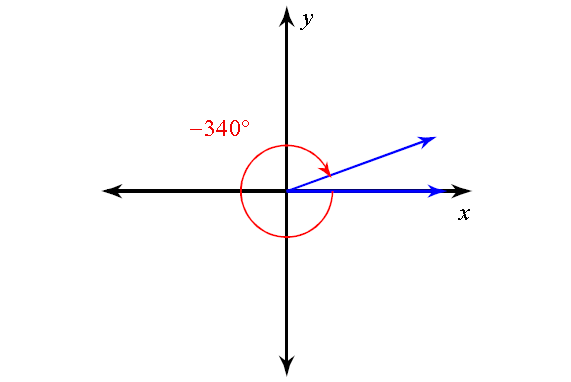
6. Answer :

The related angle for the principal angle shown above is 

=  360° - 340° 

=  20°

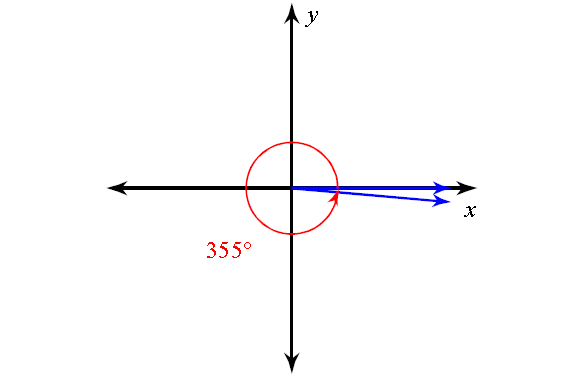
7. Answer :

The related angle for the principal angle shown above is 

=  360° - 355° 

=  5°

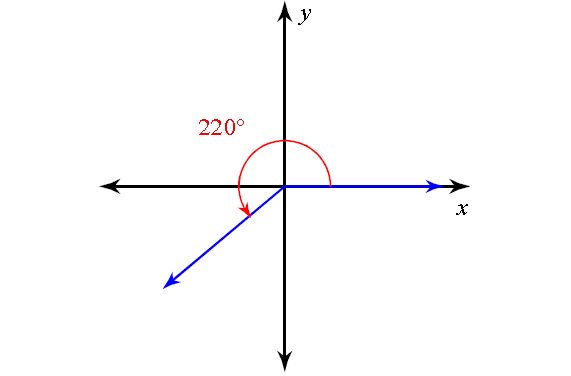
8. Answer :

The related angle for the principal angle shown above is 

=  360° - 220° 

=  140°

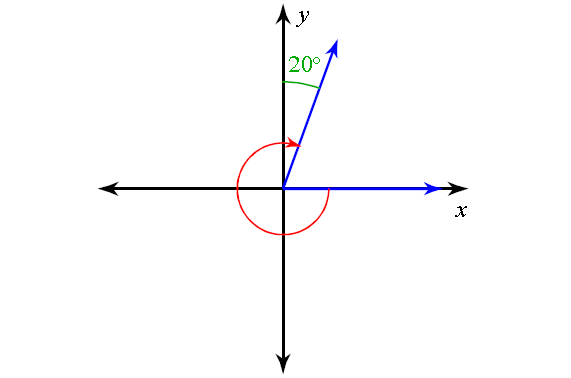
9. Answer :

The measure of principal angle of the angle shown above is 

=  (-270°) + (-20°) 

=  -270° - 20°

=  -290°

10. Answer :

The measure of principal angle of the angle shown above is 

=  90° + 30° 

=  120°

11. Answer :

300° lies between 270° and 360° 

So, the terminal side of 300° lies in the fourth quadrant.

12. Answer :

40° lies between 0° and 90° 

So, the terminal side of 40° lies in the first quadrant.

13. Answer :

Because the given angle is negative, we have to find the related angle for -222°. 

The related angle for the angle -222° is  

=  360° - 222° 

=  138°

138° lies between 90° and 180°

So, 138° lies in the second quadrant.

Because the related angle 138° lies in the first quadrant, its principal angle -222° will also lie in the same first quadrant.   

Therefore, the terminal side of -222° lies in the second quadrant.

14. Answer :

Because the given angle is negative, we have to find the related angle for -30°. 

The related angle for the angle -30° is  

=  360° - 30° 

=  330°

330° lies between 270° and 360°

So, 330° lies in the fourth quadrant.

Because the related angle 330° lies in the fourth quadrant, its principal angle -30° will also lie in the same fourth quadrant.   

Therefore, the terminal side of -30° lies in the fourth quadrant.

15. Answer :

103° lies between 90° and 180°.

So, the terminal side of 103° lies in the second quadrant.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.