ANGLES IN STANDARD POSITION

An angle is said to be in standard position, if it is drawn in the xy-plane with its vertex at the origin and its initial side is along the positive x-axis. 

Examples of angles in standard position :

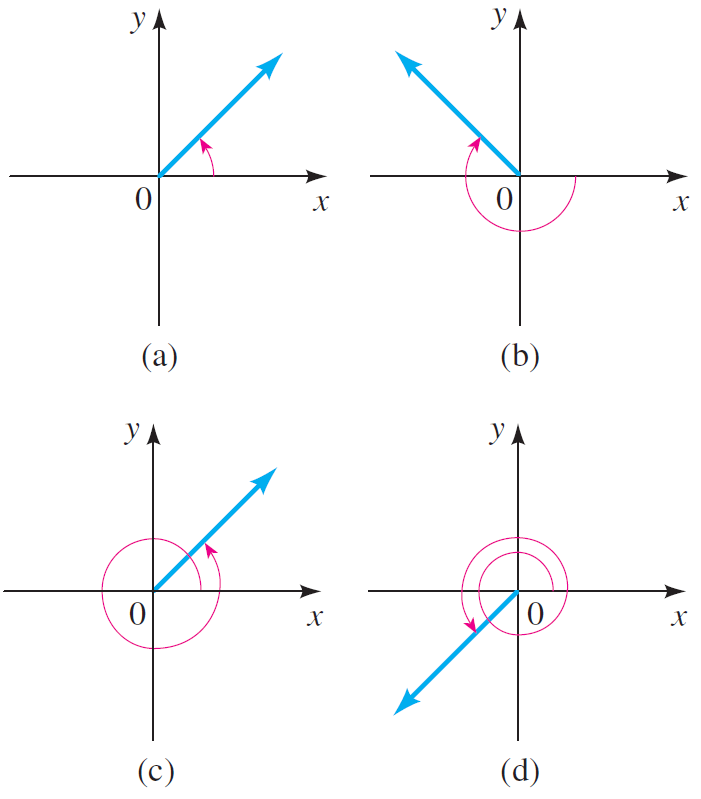
Coterminal Angles

Two angles in standard position are coterminal, if their terminal sides coincide.

The two angles shown below are coterminal. Because their terminal sides coincide. 

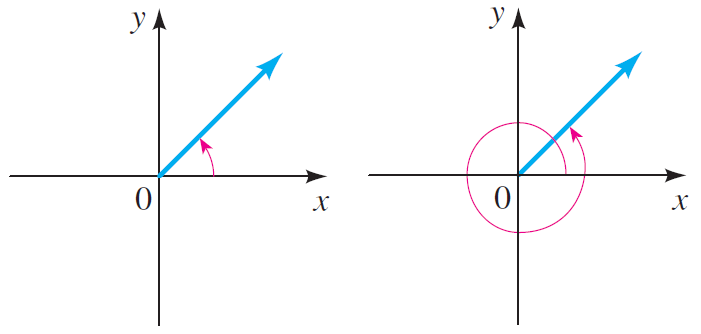
An angle is said to be in the first quadrant, if in the standard position, its terminal side falls in the first quadrant.

Similarly, we can define for the other three quadrants.

Angles in standard position having their terminal sides along the x-axis or y-axis are called quadrantal angles.

Thus, 0°, 90°, 180°, 270° and 360° are quadrantal angles.

The degree measurement of a quadrantal angle is a multiple of 90°.

Division of Quadrants

(90° - θ) -------> I st Quadrant

(90° + θ) and (180° - θ) -------> II nd Quadrant

(180° + θ) and (270° - θ) -------> III rd Quadrant

(270° + θ), (360° - θ) and (- θ) -------> IV th Quadrant

More clearly, 

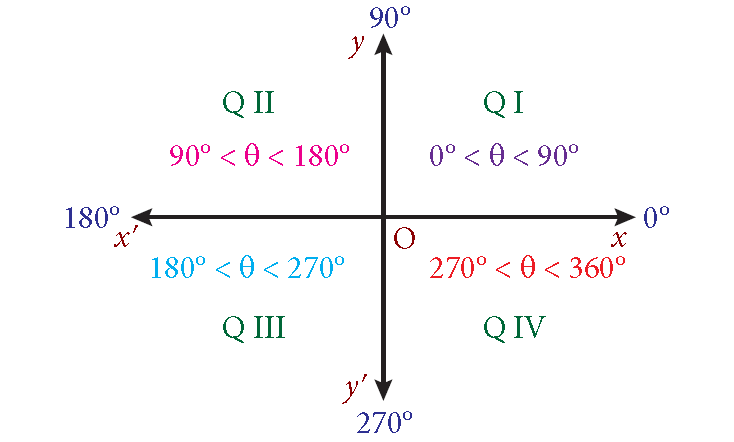
ASTC Rule

The trigonometric ratios sinθ, cosθ, tanθ, cscθ, secθ and cotθ will have different signs (positive or negative) based the quadrant where the the terminal side of the angle θ falls. 

It can be easily remembered by ASTC rule. 

This is nothing but "all sin tan cos" rule in trigonometry. 

The "all sin tan cos" rule can be remembered easily using the following phrases.

All Sliver Tea Cups 

or

All Students Take Calculus

ASTC formula has been explained clearly in the figure shown below.

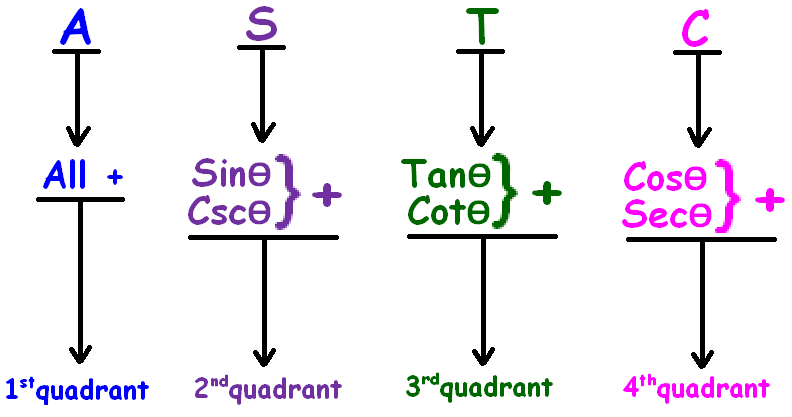
More clearly, 

In the first quadrant (0° to 90°), all trigonometric ratios are positive.

In the second quadrant (90° to 180°), sin and csc are positive and other trigonometric ratios are negative.

In the third quadrant (180° to 270°), tan and cot are positive and other trigonometric ratios are negative.

In the fourth quadrant (270° to 360°), cos and sec are positive and other trigonometric ratios are negative.

Reference Angle

Let A be an angle in standard position. The reference angle B associated with A is the acute angle formed by the terminal side of A and the x-axis.

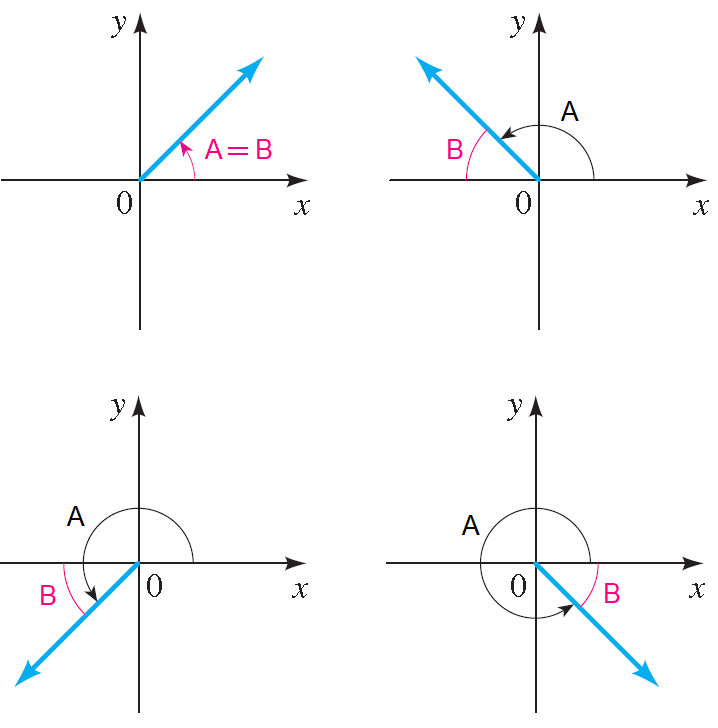
Example :

Find the reference angle for θ = 240°.

Solution :

The angle 240° has its terminal side in quadrant III, as shown below.

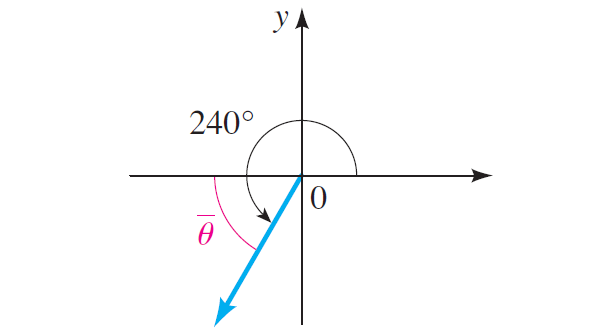
The reference angle is therefore

240° - 180°  =  60°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.