ANGLES OF A QUADRILATERAL
Like triangles, quadrilaterals have both interior and exterior angles. If we draw a diagonal in a quadrilateral, you divide it into two triangles as shown below.
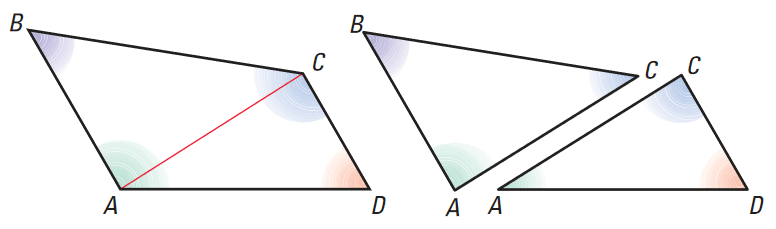
Each of the triangle above has interior angles with measures that add up to 180°.
So we can conclude that the sum of the measures of the interior angles of a quadrilateral is 2(180°), or 360°.
Find the values of the variables in the following quadrilaterals :
Example 1 :
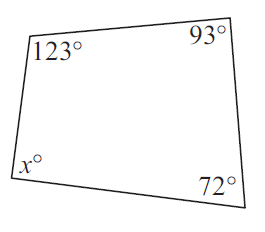
Solution :
In a quadrilateral,
Sum of interior angles = 360
123 + 93 + 72 + x = 360
x + 288 = 360
x = 360-288
x = 72
So, the missing angle is 72.
Example 2 :
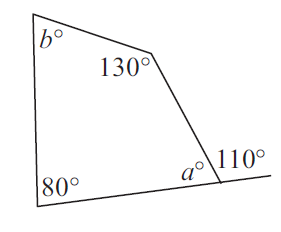
Solution :
a + 110 = 180 (linear pair)
a = 70
<a + 80 + 130 + <b = 360
70+80+130+<b = 360
<b = 360-280
<b = 80
Example 3 :
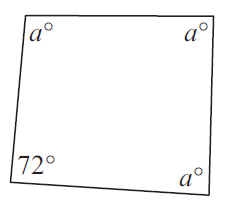
Solution :
<a+<a+<a+72 = 360
3<a = 360-72
3<a = 288
<a = 93
So, angle a is 93.
Example 4 :
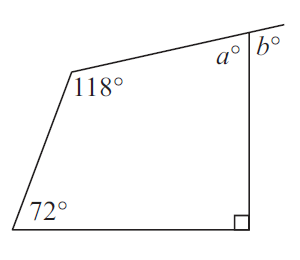
Solution :
In a quadrilateral,
72+118+90+<a = 360
280+<a = 360
<a = 360-280
<a = 80
<a+<b = 180
80+<b = 180
<b = 100
Example 5 :
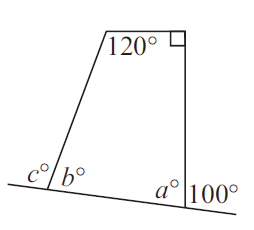
Solution :
<a+100 = 180
<a = 180-100
<a = 80
In a quadrilateral,
120+90+<b+80 = 360
290+<b = 360
<b = 360-290
<b = 70
<b+<c = 180
70+<c = 180
<c = 110
So, <a = 80, <b = 70 and <c = 110.
Example 6 :
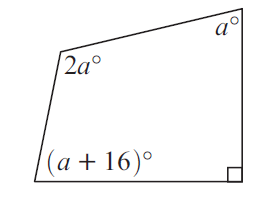
Solution :
In a quadrilateral, sum of interior angles is 360.
2a + a + 90 + (a+16) = 360
4a+106 = 360
4a = 360-106
4a = 244
a = 61
Example 7 :
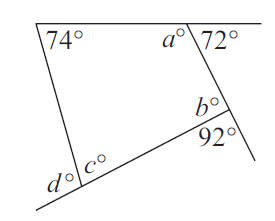
Solution :
<a+74 = 180 (linear pair)
<a = 180-74
<a = 106
<b+92 = 180(linear pair)
<b = 180-92
<b = 88
<a + 74 + <b + <c = 360
106+74+88+<c = 360
268+<c = 360
<c = 360-268
<c = 92
<c+<d = 180
92+<d = 180
<d = 180-92
<d = 88
So, <a = 106, <b = 88, <c = 92 and <d = 88.
Example 8 :
Two adjacent sides AB and BC of a parallelogram ABCD are in the ratio 5 : 3. If the perimeter is 200 cm, what is the length of AB and BC ?
(a) 25 cm & 50 cm (b) 40 cm & 37.5 cm
(c) 62.5 cm & 37.5 cm (d) 60 cm & 62.5 cm
Solution :
The given quadrilateral is in the shape of parallelogram. In the shape parallelogram, the opposite sides will be equal.
The adjacent sides are in the ratio 5 : 3. The sides are 5x and 3x.
Perimeter of parallelogram = 200 cm
2 (5x + 3x) = 200
2(8x) = 200
x = 200/16
x = 12.5
5x = 5(12.5) ==> 62.5 cm
3x = 3(12.5) ==> 37.5 cm
The side lengths are 62.5 cm and 37.5 cm. Option c is correct.
Example 9 :
One angle of a parallelogram is 60°. Find its opposite angle and the adjacent angle.
Solution :
In a parallelogram, the opposite sides are parallel and equal.
Since the opposite sides are parallel, the sum of co-interior angles is 180 degree.
Let x be the adjacent angle.
60 + x = 180
x = 180 - 60
x = 120
Example 10 :
ABCD is a trapezium with AB || DC. If ∠A = 50°, then find ∠D.
Solution :
∠A = 50°
AB and DC are parallel, then ∠A and ∠D are co-interior angles.
∠A + ∠D = 180
50 + ∠D = 180
∠D = 180 - 50
∠D = 130
Example 11 :
Four angles of quadrilaterals are in the ratio 3 : 4 : 5 : 6. Find its angles.
Solution :
Since the angles are in the ratio 3 : 4 : 5 : 6. Then the angles are 3x, 4x, 5x and 6x.
Sum of the interior angles of a quadrilateral = 360
3x + 4x + 5x + 6x = 360
18x = 360
x = 360/18
x = 20
3x = 3(20) ==> 60
4x = 4(20) ==> 80
5x = 5(20) ==> 100
6x = 6(20) ==> 120
So, the angle measures are 60, 80, 100 and 120.
Example 12 :
ABCD is a rhombus with ∠DAB = 56, determine ∠DBC
Solution :
In rhombus all sides will be equal and adjacent angles are supplementary.
∠DAB + ∠DBC= 180
56 + ∠DBC = 180
∠DBC = 180 - 56
∠DBC = 124
Example 13 :
In the following diagram of isosceles trapezoid ∠A = 46 . Find the measure of all of the remaining angles.
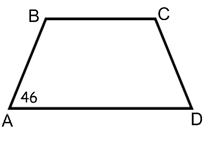
Solution :
∠A = 46
Since the shape is an isosceles trapezoid, two angle measures will be equal.
∠A = 46 and