APPLICATIONS OF PROPORTIONS WORKSHEET
Problem 1 :
In the diagram shown below ΔRST ∼ ΔBCD. Find the length of BC.
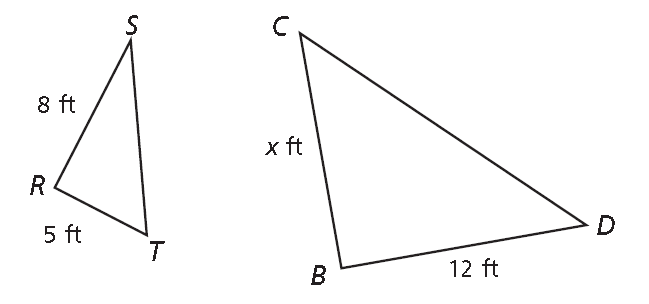
Problem 2 :
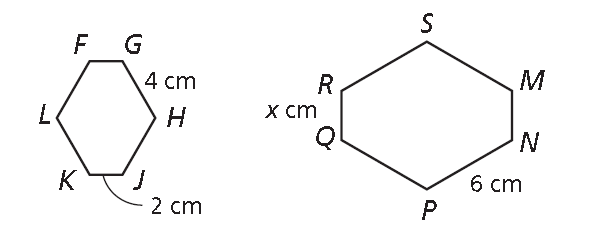
In the diagram shown below FGHJKL ∼ MNPQRS. Find the length of QR.
Problem 3 :
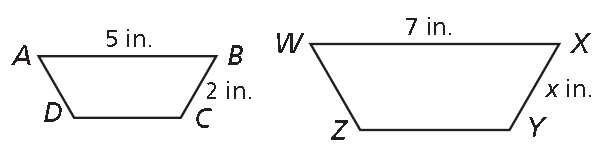
In the diagram shown below ABCD ∼ WXYZ. Find the length of XY.
Problem 4 :
A totem pole casts a shadow 45 feet long at the same time that a 6-foot-tall man casts a shadow that is 3 feet long. Write and solve a proportion to find the height of the totem pole.
Problem 5 :
Every dimension of a 2-by-4-inch rectangle is multiplied by 1.5 to form a similar rectangle. How is the ratio of the perimeters related to the ratio of corresponding sides? How is the ratio of the areas related to the ratio of corresponding sides?
Problem 6 :
Every dimension of a cylinder with radius 4 cm and height 6 cm is multiplied by ½ to form a similar cylinder. How is the ratio of the volumes related to the ratio of corresponding dimensions?

1. Answer :
R corresponds to B, S corresponds to C, and T corresponds to D.
RT/BD = RS/BC
5/12 = 8/x
Use Cross Product Property.
5(x) = 12(8)
5x = 96
Because x is multiplied by 5, divide each side by 5 to undo the multiplication.
5x/5 = 96/5
x = 19.2
The length of BC is 19.2 ft.
2. Answer :
GH/NP = JK/QR
4/6 = 2/x
Use Cross Product Property.
4(x) = 6(2)
4x = 12
Because x is multiplied by 4, divide each side by 4 to undo the multiplication.
4x/4 = 12/4
x = 3
The length of QR is 3 cm.
3. Answer :
AB/WX = BC/XY
5/7 = 2/x
Use Cross Product Property.
5(x) = 7(2)
5x = 14
Because x is multiplied by 5, divide each side by 5 to undo the multiplication.
5x/5 = 14/5
x = 2.8
The length of XY is 2.8 cm.
4. Answer :
Both the man and the totem pole form right angles with the ground, and their shadows are cast at the same angle. You can form two similar right triangles.
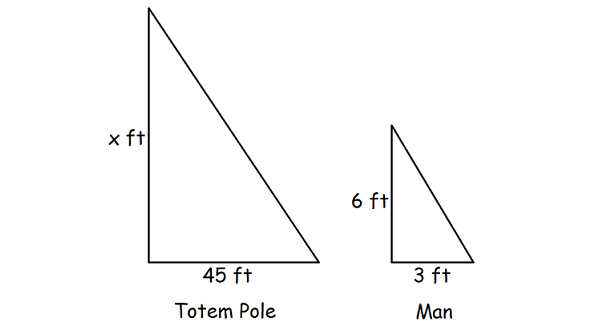
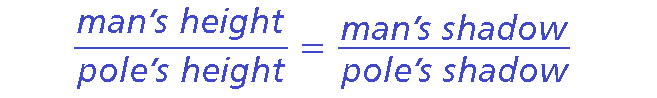
6/x = 3/45
Use Cross Product Property.
6(45) = x(3)
270 = 3x
Because x is multiplied by 3, divide each side by 3 to undo the multiplication.
270/3 = 3x/3
90 = x
The totem pole is 90 feet tall.
5. Answer :
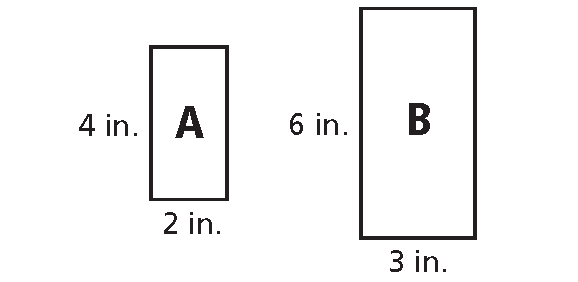
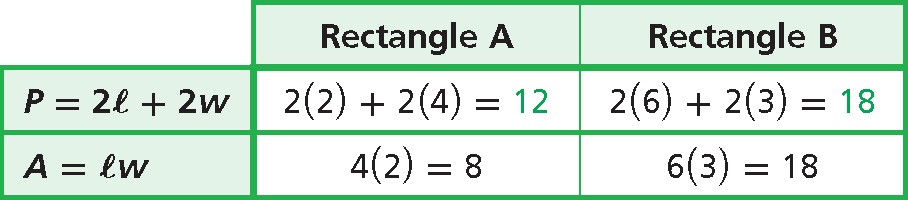
Sides :
4/6 = 2/3
Perimeters :
12/8 = 2/3
Areas :
8/18 = 4/9 = (2/3)2
The ratio of the perimeters is equal to the ratio of corresponding sides.
The ratio of the areas is the square of the ratio of corresponding sides.
6. Answer :
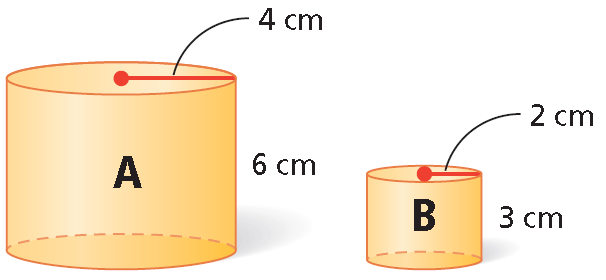

Radii :
4/2 = 2/1 = 2
Heights :
6/3 = 2/1 = 2
Volume :
96π/12π = 8/1 = 23
The ratio of the volumes is the cube of the ratio of corresponding dimensions.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Pascal Triangle and Binomial Expansion
Feb 01, 25 10:12 AM
Pascal Triangle and Binomial Expansion - Concept - Examples -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Feb 01, 25 06:26 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 106)
Feb 01, 25 06:23 AM
Digital SAT Math Problems and Solutions (Part - 106)

