APPLYING GCF AND LCM TO FRACTION OPERATIONS

Generally we have the following kinds of operations in fraction.

(i) Adding fractions 

(ii) Subtracting fractions

(iii) Multiplying fractions 

(iv) Dividing fractions

(v) Simplifying fractions

(vi) Comparing fractions

(vii) Dividing fractions by a whole number

(viii) Multiplying fractions by  whole number

In which if we want to add or subtract two or more fractions, then we may have to use the concept LCM if the denominator of those fractions are not same.

For multiplying and dividing two fractions we may have to use the concept GCF. If we want to reduce the fraction into its lowest form, then we have to apply the concept GCF.

Now let us see some examples to understand how we use the concept LCM and GCF while adding and subtracting two fractions.

Solved Examples

Example 1 :

Add   (2/3) + (1/12)

Solution :

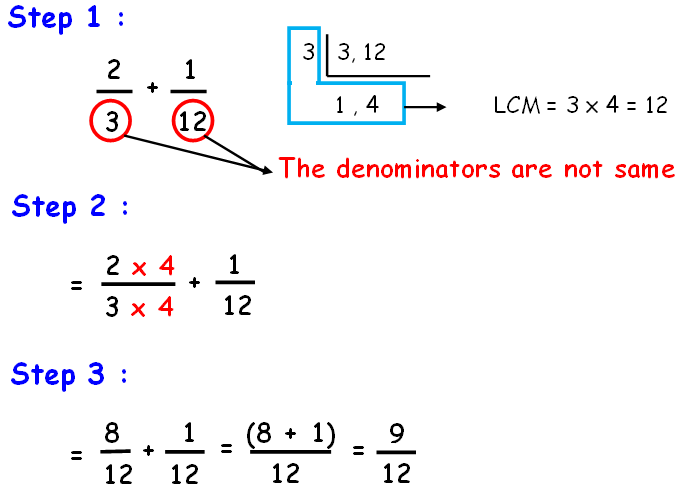
To simplify the fraction, we have to find the GCF of both numerator and denominator. 

Now we have to divide both numerator and denominator by the GCF as given below.

Therefore, the simplified form of 9/12 is 3/4. 

Example 2 :

Add (1/12) + (3/18)

Solution :

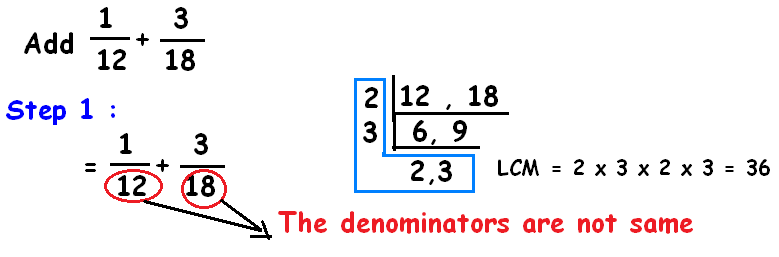
Since the denominators are not same, we have to take LCM to make the denominators same.

To simplify the fraction, we have to find the GCF of both numerator and denominator. 

Now we have to divide both numerator and denominator by the GCF as given below.

Subtracting Two Fractions using LCM - Example

If the denominators of the fractions are not co-prime (there is a common divisor other than 1), we have to apply this method.

Fro example, let us consider the two fractions 5/12,  1/20.

In the above two fractions, denominators are 12 and 20.

For 12 and 20, if there is at least one common divisor other than 1, then 12 and 20 are not co-prime.

For 12 & 20, we have the following common divisors other than 1.

2 & 4

So 12 and 20 are not co-prime.

In the next step, we have to find the L.C.M (Least common multiple) of 12 and 20.

12  =  2² x 3

20  =  2² x 5

When we decompose 12 and 20 in to prime numbers, we find 2, 3 and 5 as prime factors for 12 and 20. 

To get L.C.M of 12 and 20, we have to take 2, 3 and 5 with maximum powers found above.

So, L.C.M of 12 and 20  is

=  2² x 3 x 5

=  4 x 3 x 5

=  60

Now we have to make the denominators of both the fractions to be 60 and subtract the two fractions 5/12 and 1/20 as given below.

Multiplying Two Fractions - Example

To multiply two or more fractions, we have to multiply the numerators with numerators and denominators with denominators.

If it is possible we can simplify the fraction into its lowest form using GCF.

Example : 

Multiply (3/20) and (30/12).

Solution :

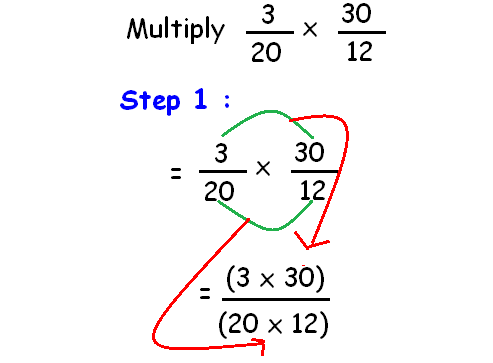
Considering the numerators and denominators we can simplify the above fraction by using the concept GCF.

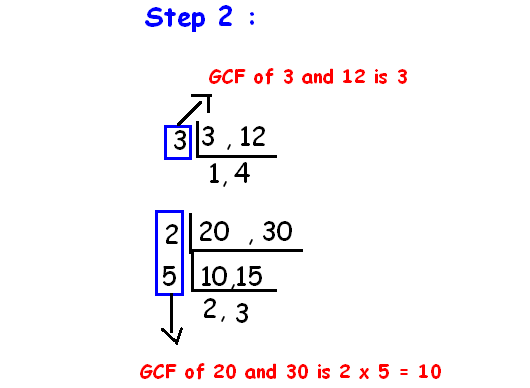
By simplifying the given fractions using GCF, We get

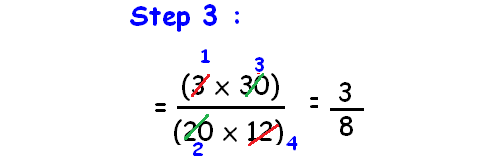
So the final answer is 3/8.

Simplifying Fractions Using GCF - Examples

Example :

Simplify 42/60 in simplest form

Solution :

Step 1 :

Write the two numbers on one line

Step 2 :

Draw the L shape

Step 3 :

Divide out common prime numbers starting from the smallest.

7 and 10 is not divisible by any common number.

7/10 is the simplified form of the given fraction 42/60.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.