APPLYING PROPERTIES OF CHORD EXAMPLES

Properties of Chords of in a Circle

Property 1 :

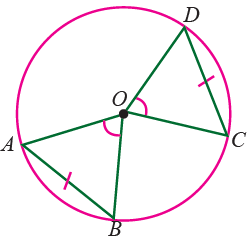
Equal chords of a circle subtend equal angles at the center.

∠AOB  =  ∠DOC

Property 2 :

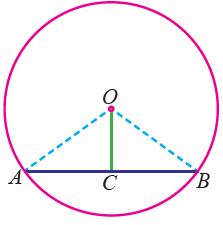
Perpendicular from the center of a circle to a chord bisects the chord.

AC  =  BC

Property 3 :

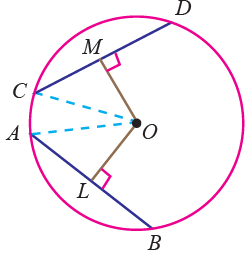
Equal chords of a circle are equidistant from the center.

OM  =  OL

Property 4 :

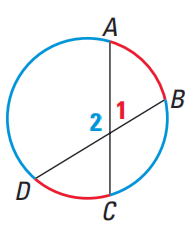
If two chords intersect inside a circle, then the measure of each angle formed is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle.

m∠1  =  (1/2) (Measure arcCD+measure of arcAB)

m∠2  =  (1/2) (Measure arcBC+measure of arcCD)

Property 5 :

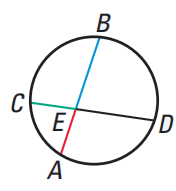
If two chords intersect inside a circle, then the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.

EA ⋅ EB  =  EC ⋅ ED

Examples

Example 1 :

Find the values of x in the diagram shown below.

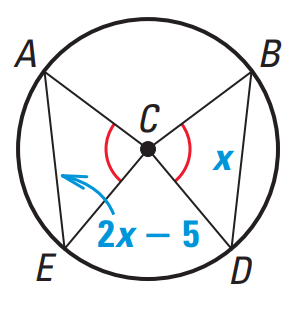
Solution :

Equal chords of a circle subtend equal angles at the center.

In the above diagram, 

∠ACE  =  ∠BCD

Then

AE  =  BD

2x - 5  =  x

Subtract x from each side.  

x - 5  =  0

Add 5 to each side.  

x  =  5

Example 2 :

Find the values of x in the diagram shown below.

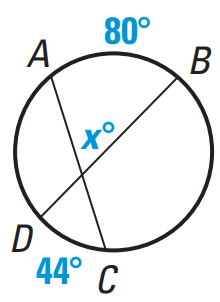
If two chords intersect inside a circle, then the measure of each angle formed is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle.

x  =  (1/2) [measure of arc AB + measure of arc DC]

x  =  (1/2) [80 + 40]

x  =  (1/2)(120)

x  =  60

Example 3 :

Find the values of x in the diagram shown below.

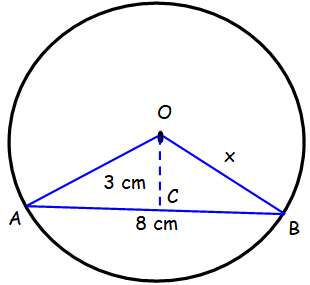
Perpendicular from the centre of a circle to a chord bisects the chord.

AC  =  BC  =  4 cm

In triangle OCB,

OB²  =  OC² + BC²

x²  =  3² + 4²

x²  =  9 + 16

x²  =  25

x  =  √25

x  =  5 cm

Example 4 :

Find the values of x in the diagram shown below.

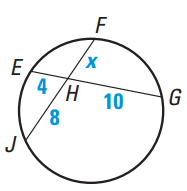
Solution :

EH ⋅ HG  =  JH ⋅ HF

4 ⋅ 10  =  8 ⋅ x

x  =  (4 ⋅ 10) / 8

x  =  40/8

x  =  5

Example 5 :

AB is a diameter of the circle below. If BC = 2 m and AB = 9 m, find the exact length of AC . 

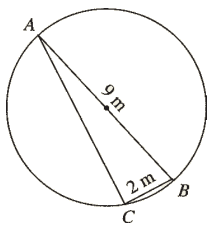
Solution :

In triangle ABC,

∠BCA  =  90° 

By Pythagorean theorem, 

AB²  =  AC² + BC²

9²  =  AC² + 2²

81  =  AC² + 4

Subtract 4 from each side. 

77  =  AC²

√77  =  √AC²

√77  =  AC

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.