ARC AND ANGLE RELATIONSHIPS IN CIRCLES

When chords, secants, and tangents intersect in a circle (Figure 1), on a circle (Figure 2), or outside of a circle (Figure 3), special relationships exist between the angle and arc measures formed.

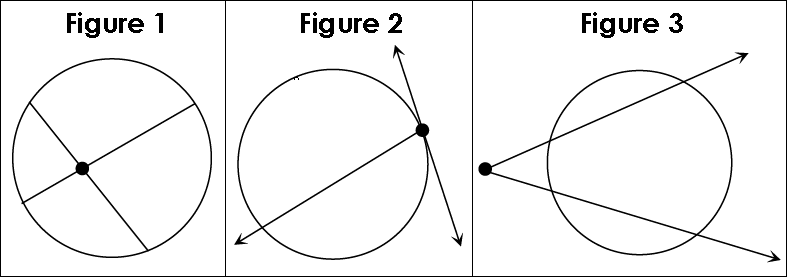
Interior Intersections

If two secants or chords intersect inside a circle, then the measure of the angle formed is equal to half the sum of the measures of the intercepted arcs.

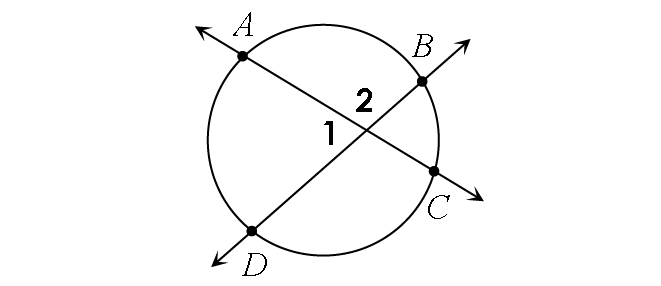
In the diagram above, 

m∠1 = ½ ⋅ (m∠arc AD + m∠arc BC)

m∠2 = ½ ⋅ (m∠arc AB + m∠arc CD)

Example 1 :

Find m∠AED. 

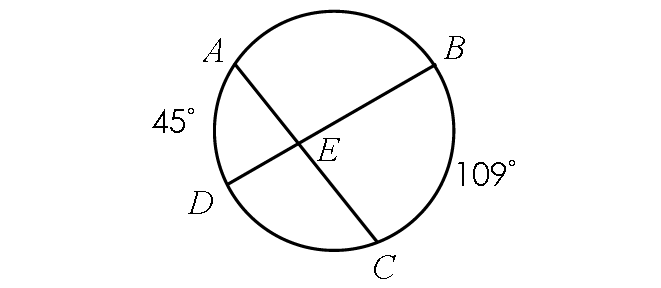
Solution :

m∠AED = ½ ⋅ (m∠arc AD + m∠arc BC)

Substitute. 

m∠AED = ½ ⋅ (45° + 109°)

m∠AED = ½ ⋅ 154°

m∠AED = 77°

Example 2 : 

Find m∠YWX. 

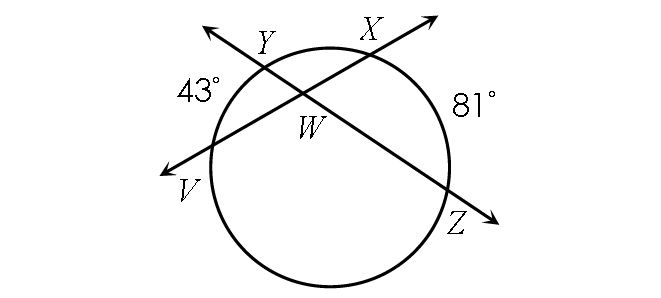
Solution :

Find m∠VWY : 

 m∠VWY = ½ ⋅ (m∠arc VY + m∠arc XZ)

m∠VWY = ½ ⋅ (43° + 81°)

m∠VWY = ½ ⋅ 124°

m∠VWY = 62°

Find m∠YWX :

m∠VWY and m∠YWX are linear pair. 

Then, 

m∠VWY + m∠YWX = 180°

Substitute m∠VWY = 62°. 

62° + m∠YWX = 180°

Subtract 62° from each side. 

m∠YWX = 118°

Example 3 : 

Find m∠arc CDE. 

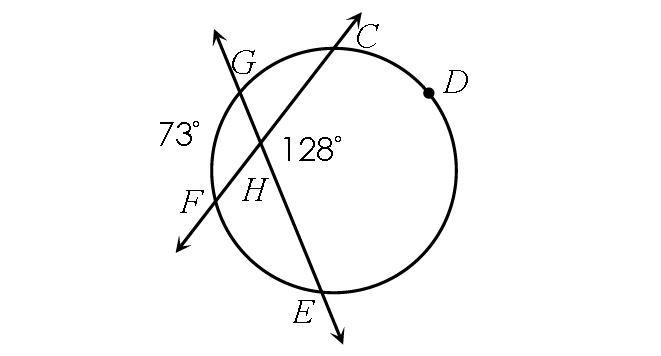
Solution :

½ ⋅ (m∠arc GF + m∠arc CDE) = m∠CHE

Substitute. 

½ ⋅ (73° + m∠arc CDE) = 128°

Multiply each side by 2.

73° + m∠arc CDE = 256°

Subtract 73° from each side. 

m∠arc CDE = 183°

Video Lesson 1

Video Lesson 2

On the Circle Intersections

If a secant and a tangent intersect at the point of tangency, then the measure of each angle formed is equal to half the measure of its intercepted arc.

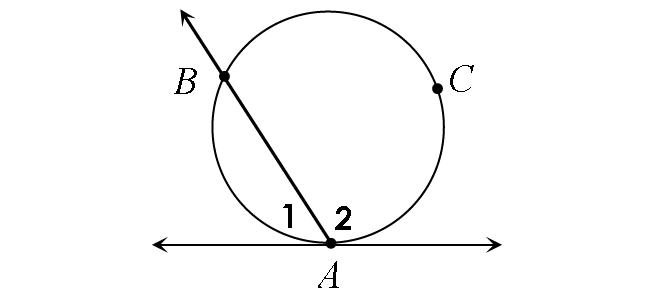
In the diagram above, 

m∠1 = ½ ⋅ m∠arc AB

m∠2 = ½ ⋅ m∠arc ACB

Example 4 :

Find m∠DEG. 

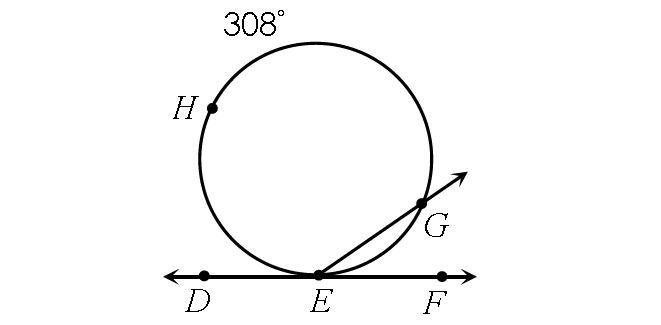
Solution :

m∠DEG = ½ ⋅ m∠arc EHG

Substitute. 

m∠DEG = ½ ⋅ 308°

m∠DEG = 154°

Example 5 :

Find m∠arc KNM. 

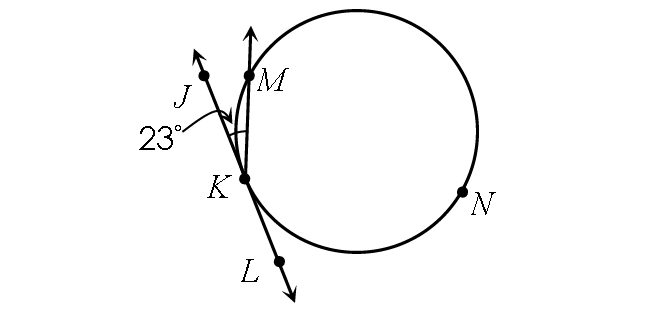
Solution :

Find m∠arc KM :

½ ⋅ m∠arc KM = m∠JKM

Substitute. 

½ ⋅ m∠arc KM = 23°

Multiply each side by 2. 

m∠arc KM = 46°

In the circle above,

m∠arc KM + m∠arc KNM = 360°

Substitute. 

46° + m∠arc KNM  =  360°

Subtract 46° from each side.

m∠arc KNM = 314°

Exterior Intersections

If secants and/or tangents intersect on the exterior of a circle, then the measure of the angle formed is equal to half the difference of the intercepted arcs.

Two Secants

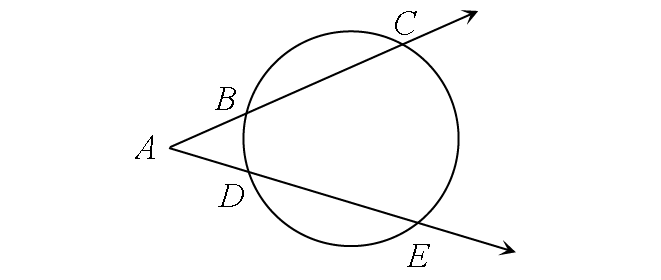
m∠A = ½ ⋅ (m∠arc CE - m∠arc BD)

Secant and Tangent

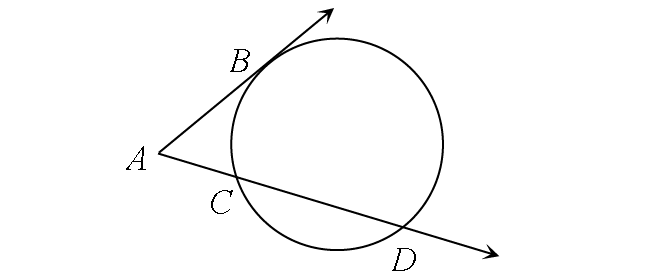
m∠A = ½ ⋅ (m∠arc BD - m∠arc BC)

Two Tangents

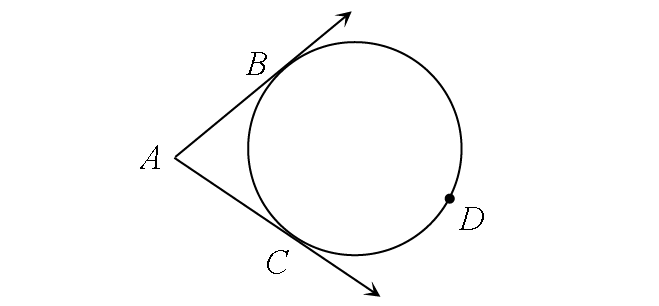
m∠A = ½ ⋅ (m∠arc BDC - m∠arc BC)

Example 6 :

Find m∠KLM. 

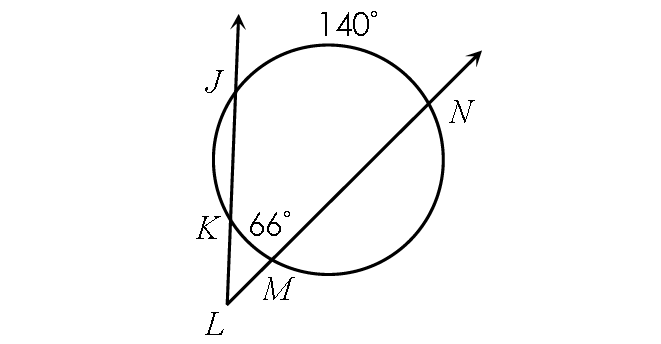
Solution :

m∠KLM = ½ ⋅ (m∠arc JN - m∠arc KM)

Substitute. 

m∠KLM = ½ ⋅ (140° - 66°)

m∠KLM = ½ ⋅ 74°

m∠KLM = 37°

Example 7 :

Find m∠BCD. 

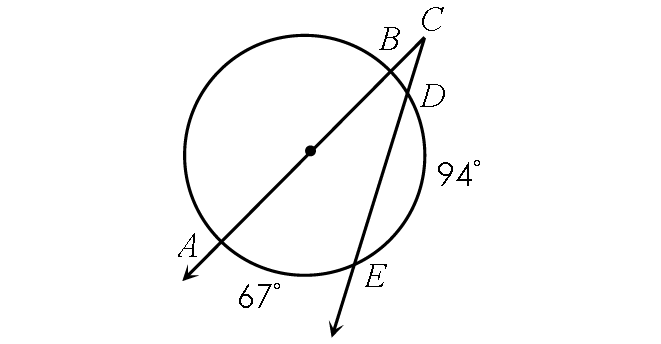
Solution :

In the circle above,

m∠arc BD + m∠arc DE + m∠arc EA = 180°

Substitute. 

m∠arc BD + 94° + 67° = 180°

m∠arc BD + 161° = 180°

Subtract 161° from each side. 

m∠arc BD = 19°

Finding m∠BCD : 

  m∠BCD = ½ ⋅ (m∠arc AE - m∠arc BD)

Substitute. 

m∠BCD = ½ ⋅ (67° - 19°)

m∠BCD = ½ ⋅ 48°

m∠BCD = 24°

Example 8 :

Find m∠KLM. 

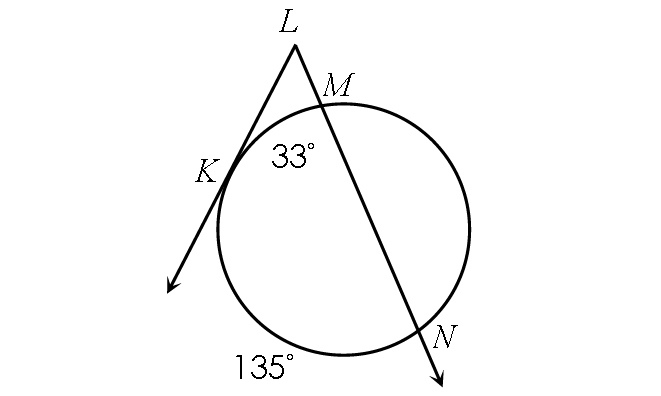
Solution :

m∠KLM = ½ ⋅ (m∠arc KN - m∠arc KM)

Substitute. 

m∠KLM = ½ ⋅ (135° - 33°)

m∠KLM = ½ ⋅ 102°

m∠KLM = 51°

Example 9 :

Find m∠CDE. 

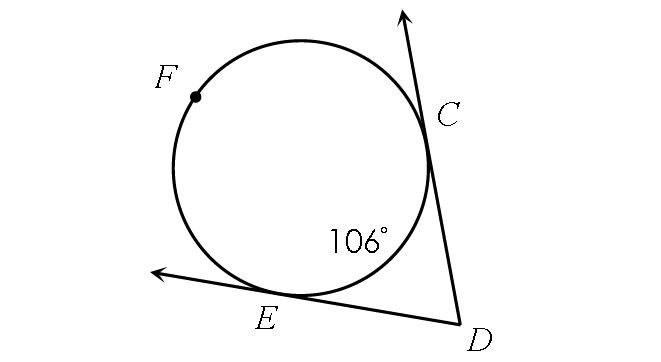
Solution :

In the circle above,

m∠arc CFE + m∠arc CE = 360°

Substitute. 

m∠arc CFE + 106° = 360°

Substitute 106° from each side. 

m∠arc CFE = 254°

Finding m∠CDE : 

m∠CDE = ½ ⋅ (m∠arc CFE - m∠arc CE)

Substitute. 

m∠CDE = ½ ⋅ (254° - 106°)

m∠KLM = ½ ⋅ 148°

m∠KLM = 74°

Example 10 :

Find m∠arc MK. 

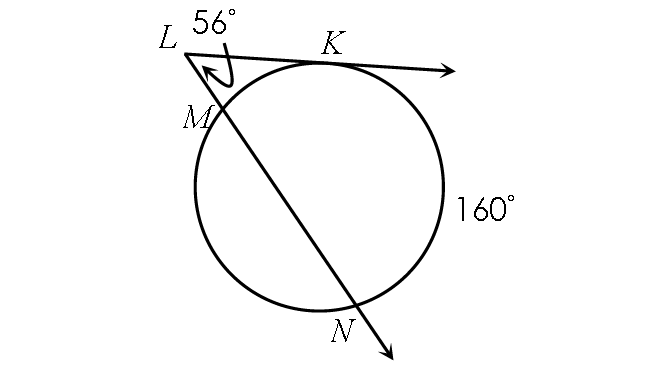
½ ⋅ (m∠arc NK - m∠arc MK) = m∠MLK

Substitute. 

½ ⋅ (160° - m∠arc MK) = 56°

Multiply each side by 2. 

160° - m∠arc MK = 112°

Subtract 160° from each side.  

- m∠arc MK = -48°

Multiply each side by -1. 

m∠arc MK = 48°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.