ARC MEASURE AND ARC LENGTH

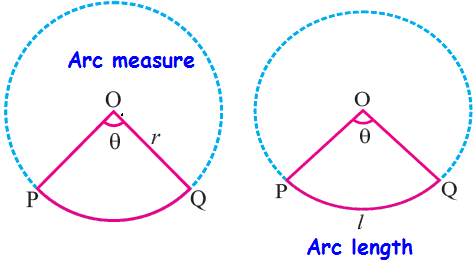
An arc measure is the measure of an angle that the arc creates at the center of the circle. This measure can be given in degrees.

Arc length of a sector is the length of the portion on the circumference of the circle intercepted between the bounding radii and is denoted by l.

Formula to find the length of the arc l is 

 l  =  (θ/360) x 2πr

To solve for arc measure, we have to solve θ in the above formula.   

Example 1 :

The radius of a sector is 42 cm and its sector angle is 60°. Find its arc length

Solution :

Radius of the sector  =  42 cm

Sector angle θ  =  60°

Length of the arc is 

l  =  (θ/360) x 2Πr

  =  (60°/360°) x 2 x (22/7) x 42

  =  (1/6) x 2 x 22 x 6

  =  44 cm

Example 2 :

The arc length of a sector is 66 cm and the central angle is 30°. Find its radius.

Solution :

Arc length of sector  =  66 cm

Sector angle θ  =  30°

Formula for length of the arc is

l  =  (θ/360) x 2Πr

Substitute the known values and solve for r.

66  =  (30°/360°) x 2 x (22/7) x r

 66  =  (1/12) x 2 x 22 x r

r  =  (66 x 12)/(2 x 22)

r  =  126 cm

Example 3 :

The length of arc of a sector is 22 cm and its radius is 10.5 cm. Find its central angle.

Solution :

Arc length of sector  =  22 cm

radius  =  10.5 cm 

Formula for length of the arc is

l  =  (θ/360°) x 2Πr

Substitute the known values and solve for θ.

22  =  (θ/360) x 2 x (22/7) x 10.5

 22  =  (θ/360) x 2 x 22 x 1.5

θ  =  (22 x 360)/(2 x 22 x 1.5)

=  180/1.5

θ  =  120°

Example 4 :

A pendulum swings through an angle of 30° and describes an arc length of 11 cm. Find the length of the pendulum.

Solution :

Arc length of sector  =  11 cm

sector angle  =  30°

If the pendulum swings once, then it forms a sector and the radius of the sector is the length of the pendulum.

So,

l  =  (θ/360°) x 2Πr

Substitute the known values and solve for r.

11  =  (30°/360°) x 2 x (22/7) x r

 11  =  (1/12) x 2 x (22/7) x r

r  =  (11 x 7 x 12)/(2 x 22)

r  =  7 x 3

r  =  21 cm

So, the length of pendulum is 21 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.