ARCS AND CHORDS WORKSHEET
Problem 1 :
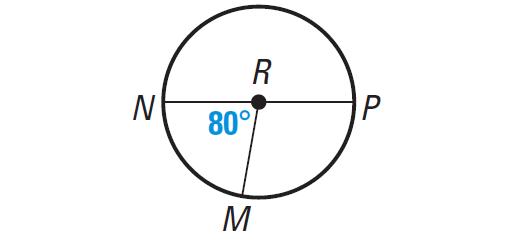
Find the measure of each arc of ⊙R.
(i) arc MN
(ii) arc MPN
(iii) arc PMN
Problem 2 :
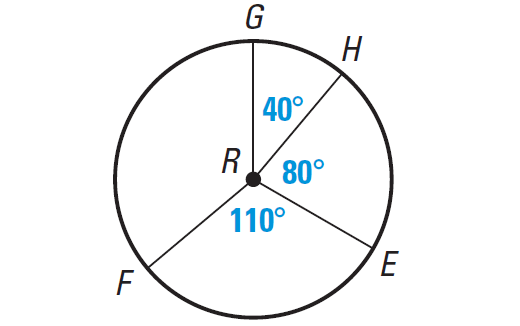
Find the measure of each arc of ⊙R.
(i) arc GE
(ii) arc GEF
(iii) arc GF
Problem 3 :
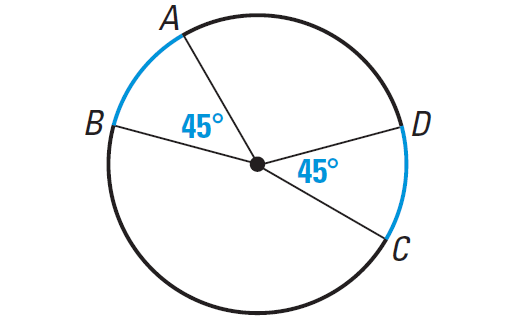
Find the measures of the blue arcs in the diagram shown below. Are they congruent ?
Problem 4 :
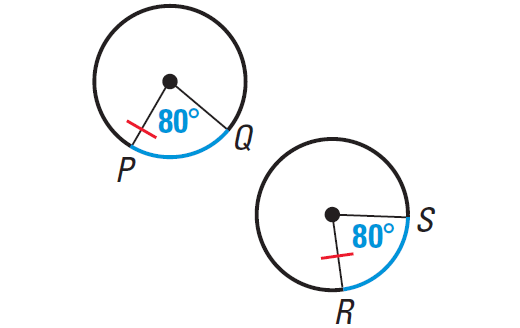
Find the measures of the blue arcs in the diagram shown below. Are they congruent ?
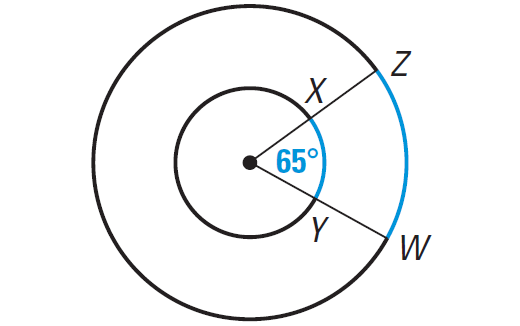
Problem 5 :
Find the measures of the blue arcs in the diagram shown below. Are they congruent ?
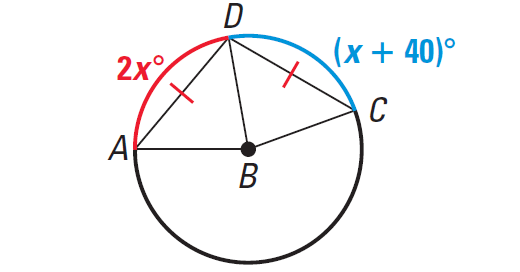
Problem 6 :
In the diagram shown below, find the value of x.
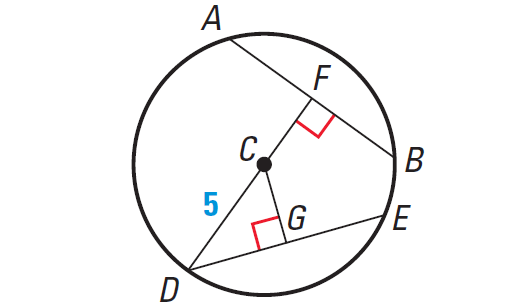
Problem 7 :
In the diagram shown below,
AB = 8, DE = 8 and CD = 5
Find CF.
Problem 8 :
A masonry hammer has a hammer on one end and a curved pick on the other end. The pick works best, if we swing it along a circular curve that matches the shape of the pick. Find the center of the circular swing.

Answers
Problem 1 :
Find the measure of each arc of ⊙R.
(i) arc MN
(ii) arc MPN
(iii) arc PMN

Solution :
Part (i) :
MN is a minor arc. So we have
measure of arc MN = m∠MN = 80°
Part (ii) :
MPN is a major arc. So we have
measure of arc MPN = m∠MPN = 360° - 80°
measure of arc MPN = 360° - 80°
measure of arc MPN = 280°
Part (iii) :
PMN is a semicircle. So we have
measure of arc PMN = m∠PMN = 180°
Problem 2 :
Find the measure of each arc of ⊙R.
(i) arc GE
(ii) arc GEF
(iii) arc GF

Solution :
Part (i) :
m∠arc GE = m∠arc GH + m∠arc HE
m∠arc GE = 40° + 80°
m∠arc GE = 120°
Part (iii) :
m∠arc GEF = m∠arc GE + m∠arc EF
m∠arc GEF = 120° + 110°
m∠arc GEF = 230°
Part (iii) :
m∠arc GF = 360° - m∠arc GEF
m∠arc GF = 360° - 230°
m∠arc GF = 130°
Problem 3 :
Find the measures of the blue arcs in the diagram shown below. Are they congruent ?

Solution :
Arcs AB and DC are in the same circle.
And, m∠arc AB = m∠arc DC = 45°. So, we have
arc AB ≅ arc DC
Problem 4 :
Find the measures of the blue arcs in the diagram shown below. Are they congruent ?

Solution :
Arc PQ and arc RS are in congruent circles.
m∠arc PQ = m∠arc RS = 80°
So, we have
arc PQ ≅ arc RS
Problem 5 :
Find the measures of the blue arcs in the diagram shown below. Are they congruent ?

Solution :
m∠arc XY = m∠arc ZW = 65°, but arc XY and arc ZW are not arcs of the same circle or of congruent circles.
So, arc XY and arc ZW are not congruent.
Problem 6 :
In the diagram shown below, find the value of x.

Solution :
Because AD ≅ DC,
arc AD ≅ arc DC
So, we have
m∠arc AD = m∠arc DC
(2x)° = (x + 40)°
Subtract x from each side.
x = 40
Problem 7 :
In the diagram shown below,
AB = 8, DE = 8 and CD = 5
Find CF.

Solution :
Because AB and DE are congruent chords, they are equidistant from the center.
So, CF ≅ CG. To find CG, first we have to find DG.
CG ⊥ DE, so CG bisects DE.
Because DE = 8, we have
DG = 8/2
DG = 4
Now, use DG to find CG.
DG = 4 and CD = 5, so ΔCGD is a 3-4-5 right angle.
So, CG = 3.
Finally, use CG to find CF.
Because CF ≅ CG, we have
CF = CG = 3
Problem 8 :
A masonry hammer has a hammer on one end and a curved pick on the other end. The pick works best, if we swing it along a circular curve that matches the shape of the pick. Find the center of the circular swing.
Solution :
Draw a segment AB, from the top of the masonry hammer to the end of the pick as shown in the diagram below. Find the midpoint C, and draw a perpendicular bisector CD. Find the intersection of CD with the line formed by the handle.
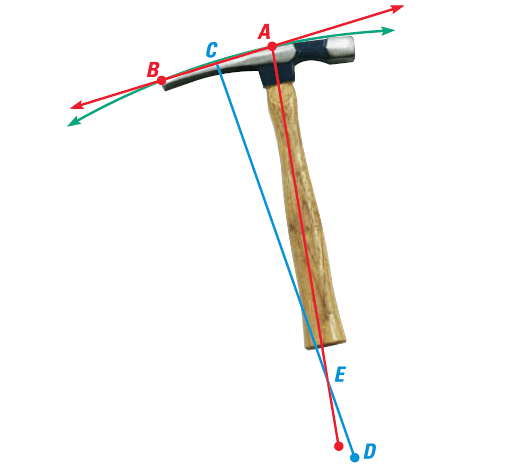
The point of intersection of CD with the line formed by the handle is the center of the swing.
So, the center of the swing lies at E.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145) -
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144)

