AREA AND PERIMETER OF A RECTANGLE WORKSHEET

Problem 1 :

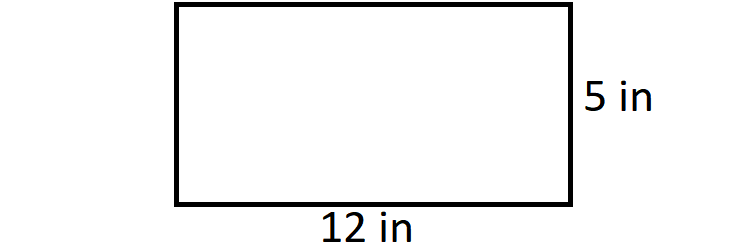
Find the perimeter and area of a rectangle of length 12 inches and width 5 inches. 

Problem 2 :

The area of a rectangle is 56 square inches. If the length is 8 inches, find the width of the rectangle.  

Problem 3 : 

The perimeter of a rectangle is 30 cm. The length is 3 more than twice the width. Find the length and width of the rectangle.  

Problem 4 :

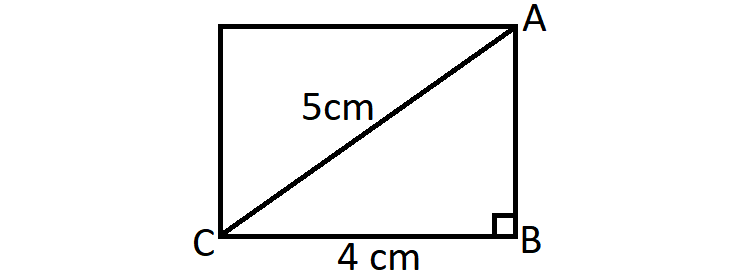
The diagonal of a rectangle is 5 cm and one of its sides is 4 cm. Find its area. 

Problem 5 : 

The poster has a border whose width is 2 cm on each side. If the printed material has the length of 6 cm and width of 8 cm, then find the area of the border. 

Answers

1. Answer :

Draw a rectangle and label the length and width. 

So, the perimeter is 34 inches and the area is 60 square inches.

2. Answer :

Given :  Area of the rectangle  =  56 sq. in

l ⋅ w  =  56

Substitute l = 8

8 ⋅ w  =  56

Divide both sides by 8.

w  =  7

So, the width is 7 inches.

3. Answer :

Step 1 :

Let w  =  x. 

Then, l  =  2x + 3

Step 2 :

Given :  Perimeter of the rectangle  =  30 cm

2l + 2w  =  30

Step 3 :

Substitute w = x and l = 2x + 3

2(2x + 3) + 2x  =  30

4x + 6 + 2x  =  30

6x + 6  =  30 

Subtract 6 from both sides.

6x  =  24

Divide both sides by 6.

x  =  4

Width  =  x  =  4

Length  =  2x + 3  =  2(4) + 3  =  11

So, the length is 11 cm and width is 4 cm. 

4. Answer :

Step 1 :

Let us assume that one of the sides given is length.

Then, l  =  4 cm. 

Step 2 :

Draw a rectangle and label the diagonal and length.

Step 3 :

To find area of a rectangle, we need the measures of length and width. We know the length and it is 4 cm. We have to find the width. 

Step 4 :

In the rectangle above, let us consider the right triangle ABC and apply Pythagorean theorem. 

AB² + BC²  =  AC²

Substitute BC  =  4 and AC  =  6.

w² + 4²  =  5²

w² + 16  =  25

Subtract 16 from both the sides.

w²  =  9

w²  =  3²

w  =  3 cm

Step 5 :

Area of the rectangle  =  l ⋅ w

Area of the rectangle  =  4 ⋅ 3 

Area of the rectangle  =  12 square cm.  

5. Answer :

Draw a sketch

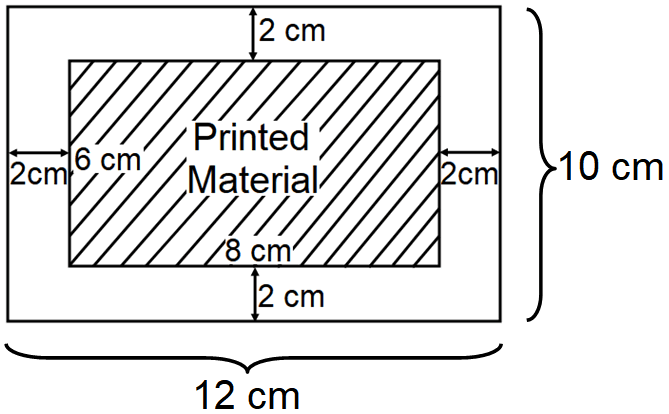
In the above diagram, to find the area of the border, we have to subtract the area of the printed material from the complete area of the poster. 

Complete area of the poster : 

=  l ⋅ w

Substitute 10 for l and 12 for w. 

=  10 ⋅ 12

=  120 cm² 

Area of the poster is 120 square cm.

Area of the printed material : 

=  l ⋅ w

Substitute 6 for l and 8 for w. 

=  6 ⋅ 8

=  48 cm² 

Area of the printed material is 48 square cm.

Area of the border :

=  Area of the poster - Area of the printed material

=  120 - 48

=  72 cm²

So, the area of the border is 72 square cm. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.