AREA AND PERIMETER OF SIMILAR FIGURES WORKSHEET

Problem 1 :

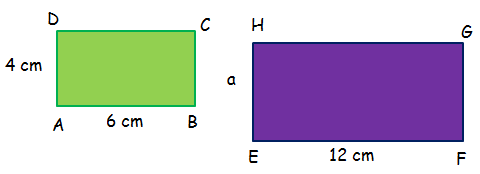
The two rectangles given below are similar. Find the perimeter of the rectangle EFGH. 

Problem 2 :

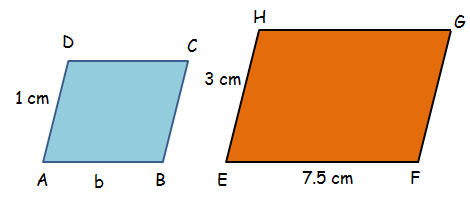
The two parallelograms shown below are similar. Find the perimeter of the parallelogram ABCD. 

Problem 3 :

The perimeters of two similar triangles is in the ratio 3 : 4. The sum of their areas is 75 cm². Find the area of each triangle.

Problem 4 :

The areas of two similar triangles are 45 cm² and 80 cm². The sum of their perimeters is 35 cm. Find the perimeter of each triangle. 

Answers

1. Answer :

Because the above rectangles ABCD and EFGH are similar, the lengths of the corresponding sides will be proportional.

AB/EF  =  AD/EH

6/12  =  4/a

1/2  =  4/a

2/1  =  a/4

Multiply each side by 12. 

(2/3) ⋅ 12  =  a

8  =  a

Perimeter of rectangle EFGH is  

=  2(l + w)

=  2(12 + 8)

=  2(20)

=  40

So, the perimeter of the rectangle EFGH is 40 cm. 

2. Answer :

Because the above parallelograms ABCD and EFGH are similar, the lengths of the corresponding sides will be proportional.

AB/EF  =  AD/EH

b/1  =  7.5/3

b  =  2.5

Perimeter of the parallelogram ABCD is  

=  2(2.5 + 1)

=  2(3.5)

=  7

So, the perimeter of the parallelogram ABCD is 7 cm. 

3. Answer :

Given :  Perimeters of two similar triangles is in the ratio

3 : 4

Then,

Perimeter of the 1^st Δ  =  3x

Perimeter of the 2^nd Δ  =  4x

And also, 

Area of 1^st Δ : Area 2^nd Δ  =  (3x)² : (4x)²

Area of 1^st Δ : Area 2^nd Δ  =  9x² : 16x²

Given : Sum of the areas is 75 cm².

Then, 

9x² + 16x²  =  75

25x²  =  75

Divide by 25 from each side. 

25x²  =  75

x²  =  3

Area of 1^st Δ  =  9(3)  =  27 cm²

Area of 2^nd Δ  =  16(3)  =  48 cm²

4. Answer :

Ratio between the areas of two triangles is

=  45 : 80

=  9 : 16

Then, the ratio between the perimeters of two triangles is

=  √9 : √16

=  3 : 4

So,

Perimeter of 1^st Δ  =  3x

Perimeter of 2^nd Δ  =  4x

Given : Sum of the perimeters is 35 cm.

Then,

3x + 4x  =  35

7x  =  35

x  =  5

So,

Perimeter of 1^st Δ  =  3x  =  3(5)  =  15 cm

Perimeter of 2^nd Δ  =  4x  =  4(5)  =  20 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.