AREA AND VOLUME OF SIMILAR FIGURES EXAMPLE PROBLEMS

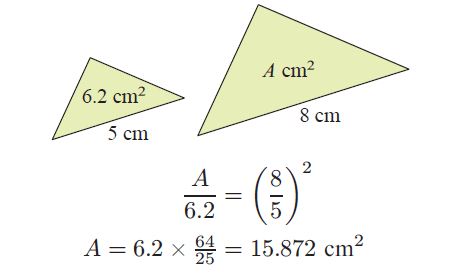
If the corresponding sides of similar figures are in the ratio k, then :

Area of image  =  k² x area of object.

For example, for the similar triangles alongside:

Example 1 :

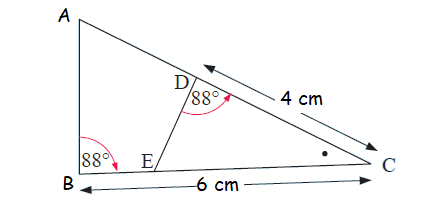
Triangle DEC has area 4.2 cm².

a) Find the area of triangle ABC.

b) Find the area of quadrilateral ABED.

Solution :

In the triangle given above, ΔABC and ΔDEC.

<BCA  =  <ECD  (A)

ABC  =  <EDC  (A)

ΔABC and ΔDEC are similar. Bases of triangle ABC and EDC are BC and DC respectively.

(i)  Area of Δ ABC/Area of Δ DEC  =  (BC/DC)²

Area of Δ ABC/4.2  =  (6/4)²

Area of Δ ABC  =  (36/16) x 4.2

=  9.45 cm²

(ii)  Area of quadrilateral AEBD  =  Area of triangle ABC - Area of triangle DEC

=  9.45-4.2

=  5.25 cm²

So, area of quadrilateral is AEBD is 5.25 cm².

Example 2 :

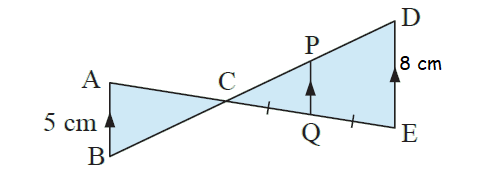
If triangle ABC has area 15 cm²:

a) find the area of ΔCDE

b) find the area of PQED.

Solution :

(a)  In triangles ABC and CDE

AB is parallel to DE

Area of ABC/Area of CDE  =  (AB/DE)²

15/Area of CDE  =  (5/8)²

15/Area of CDE  =  25/64

Area of CDE  =  15(64)/25

=  38.4 cm²

In triangles CPQ and CDE

PQ is parallel to DE

Area of ΔCPQ/area of ΔCDE  =  (CQ/CE)²

CQ  =  x and CE  =  2x

Area of ΔCPQ/38.4  =  (x/2x)²

Area of ΔCPQ  =  38.4/4

Area of ΔCPQ  =  9.6

(b)  Area of quadrilateral DPQE

  =  Area of CDE - Area of CPQ

=  38.4-9.6

=  28.8 cm²

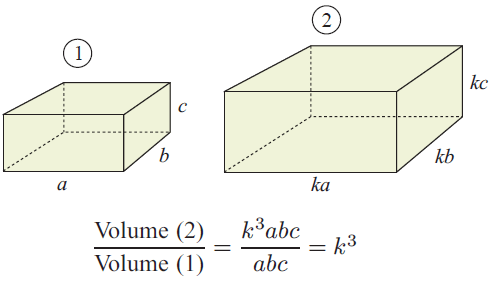
If the corresponding sides of similar solids are in the ratio k, then :

Volume of image  =  k³ x volume of object.

Example 3 :

What will happen to the volume of:

a) a sphere if the radius is doubled

b) a sphere if the radius is increased by 20%

Solution :

Volume of sphere  =  (4/3)πr³

(a)  Radius of the sphere  =  r

Radius of new sphere  =  2r

Volume of new sphere  =  (4/3)π(2r)³

 =  (4/3)π(8r³)

 =  8 x (4/3)πr³

So, volume of the new sphere will be 8 times volume of old sphere.

(b)  Radius of sphere is increased by 20%.

Radius of new sphere  =  1.20r

Volume of new sphere  =  (4/3)π(1.20r)³

 =  (4/3)π(1.728r³)

 =  1.728 x (4/3)πr³

So, volume of the new sphere will be 1.728 times volume of old sphere.

Example 4 :

Triangle A is similar to Triangle B. If the scale factor of ΔA to ΔB is 4 to 5, what is the ratio of the perimeters of ΔA to ΔB? ____________ What is the ratio of the areas of ΔA to ΔB? __________________

Solution :

Since the corresponding sides are in the ratio 4 : 5, its perimeter will also be in the same ratio,

Area of triangle A : Area of triangle B = (4 : 5)²

= 4² : 5²

= 16 : 25

So, the ratio between the area of triangles A and B is 16 : 25

Example 5 :

Pyramid X is similar to Pyramid Y. If the scale factor of X:Y is 3:7, what is the ratio of the surface areas of X:Y? __________ What is the ratio of the volumes of X:Y? ____________

Solution :

Surface area of Pyramid X : Surface area of Pyramid Y

= (3 : 7)²

= 9 : 49

Volume of Pyramid X : Volume of Pyramid Y

= (3 : 7)³

= 27 : 343

Example 6 :

The ratio of the surface areas of two similar cones is 16:49. What is the scale factor between the similar cones? __________ What is the ratio of the volumes of the similar cones? __________

Solution :

Let a and b be sides corresponding sides are cones.

Ratio between surface area of similar cone

(a/b)² = 16/49

a/b = √(16/49)

a/b = 4/7

a : b = 4 : 7

Ratio between volume of similar cone

(a/b)³ = (4/7)³

a/b = (4³/7³)

a/b = 64/343

Ratio between volume = 64 : 343.

Example 7 :

Two spheres have a scale factor of 1:3. The smaller sphere has a surface area of 16 ft². Find the surface area of the larger sphere.

Solution :

Ratio between sides lengths of sphere = 1 : 3

Let a and be the corresponding sides of sphere

Surface area of small sphere : Surface area large sphere = 1² : 3²

16/surface area of large sphere = 1/9

Surface area of large sphere = 9(16)

= 144

Example 8 :

Two rectangular prisms are similar and the ratio of their sides is 2:3. The surface area of the larger rectangular prism is 1944 cm². What is the surface area of the smaller rectangular prism?

Solution :

Ratio between corresponding sides = 2 : 3

Surface area of small rectangular prism : Surface area of small rectangular prism =

2² : 3²

Surface area of small sphere / 1944 = 4 : 9

Surface area of small sphere / 1944 = 4/9

Surface area of small sphere = (4/9) 1944

= 864 cm²

Example 9 :

The ratio of the sides of two similar cubes is 3:4. The smaller cube has a volume of 729 m³. What is the volume of the larger cube?

Solution :

Ratio between corresponding sides = 3 : 4

Volume of small cube : Volume of large cube = 3³ : 4³

729 / Volume of large cube = 27 / 64

Volume of large cube = (64/27) (729)

= 1728 m³

Example 10 :

Pyramid X is similar to pyramid Y. The Surface area of pyramid X is 135 cm², and the surface area of pyramid Y is 240 cm². If the volume of pyramid X is 189 cm³, then what is the volume of pyramid Y?

Solution :

Let a and be be the corresponding sides of Pyramid X and Pyramid Y respectively.

(a : b)² = 135/240

a² / b² = 135 / 240

a/b = √135/√240

a/b = 11.61/15.49

a/b = 0.75

Volume of small cube : Volume of large cube = (a/b)³

189/Volume of large cube = (0.75)³

Volume of large cube = 189/(0.75)³

= 450

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.