AREA AND VOLUME OF SIMILAR SHAPES EXAMPLES
If the corresponding sides of similar figures are in the ratio k, then :
Area of image = k2 x area of object
For example, for the similar triangles alongside :
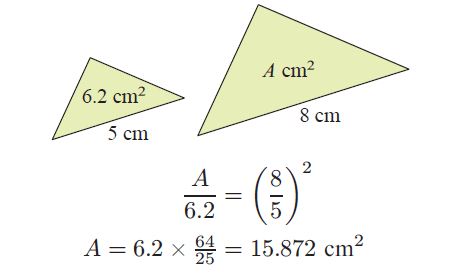
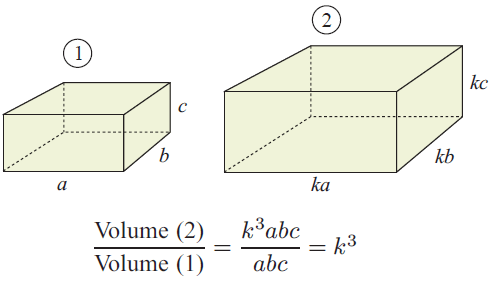
If the corresponding sides of similar solids are in the ratio k, then :
Volume of image = k3 x volume of object.
For each pair of similar figures, find the unknown area.
Example 1 :
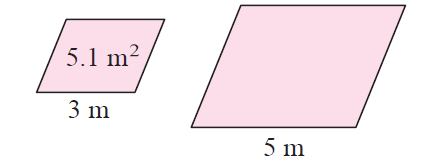
Solution :
Let A1 and A2 be the area of given figures.
A1 = 5.1 m2 and A2 = ?
Let L1 and L2 be the length of sides of shape 1 and shape 2.
L1 = 3 and L2 = 5
k = L1/L2 ==> 3/5
k2 = (3/5)2
Using the formula :
A1/A2 = (l1/l2)2
A1/A2 = (3/5)2
5.1/A2 = (9/25)
A2 = (25/9) ⋅ (5.1)
A2 = 14.16 m2
Example 2 :
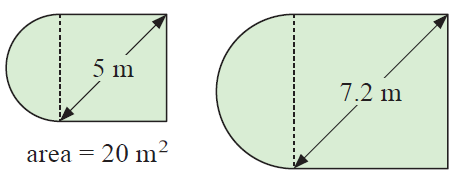
Solution :
Let A1 and A2 be the area of given figures.
A1 = 20 m2 and A2 = ?
Let L1 and L2 be the length of sides of shape 1 and shape 2.
L1 = 5 m and L2 = 7.2 m
k = L1/L2 ==> 5/7.2
k2 = (5/7.2)2
Using the formula :
A1/A2 = (5/7.2)2
20/A2 = 0.48
A2 = 20/(0.48)
A2 = 41.6 m2
Example 3 :
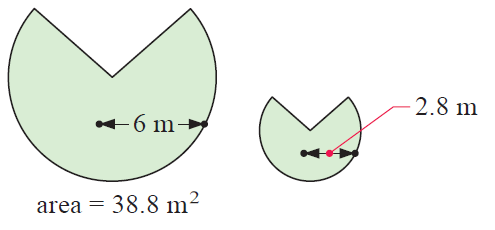
Solution :
Let A1 and A2 be the area of given figures.
A1 = 38.8 m2 and A2 = ?
Let L1 and L2 be the length of sides of shape 1 and shape 2.
L1 = 6 m and L2 = 2.8 m
k = L1/L2 ==> 6/2.8
k2 = (6/2.8)2.
Using the formula :
A1/A2 = (6/2.8)2
38.8/A2 = 4.58
A2 = 38.8/4.58
A2 = 8.47 m2
Example 4 :
In the given figure, the area of triangle BCD is 6.4 cm2. Find the area of
(a) Triangle ACE
(b) Quadrilateral ABDE
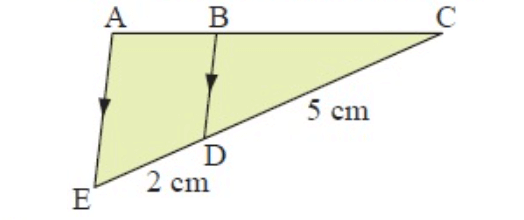
Solution :
In triangles BDC and AEC,
<BDC = <AEC
<BCD = <ACE
So, BDC is similar to AEC.
(a) Side lengths are in the ratio 5:7
k = 5/7
Area of triangle BCD = (5/7)2 area of triangle ACE
6.4 = (25/49) Area of triangle ACE
Area of triangle ACE = 6.4(49/25)
= 12.54 cm2
(b) Area of quadrilateral AECD = Area of triangle ACE - Area of triangle BCD
= 12.54-6.4
= 6.14 cm2
Example 5 :
Find
(a) The value of x
(b) The area of triangle PQT is given quadrilateral QRST has the area 22 m2
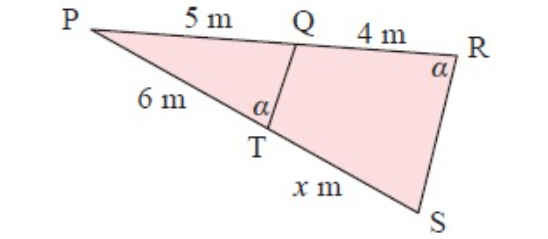
Solution :
By comparing triangles PQT and PRS.
<QPT = <RPS (A)
<PTQ = <PRS (A)
So, triangle PTQ is similar to the triangle PRS.
PQ/PS = QT/RS = PT/PR
5/(x+6) = 6/(5+4)
5/(x+6) = 6/9
5/(x+6) = 2/3
15 = 2x+12
2x = 3
x = 1.5 cm.
(b) Ratio of side length PQT to PRS is 2/3.
k = 2/3
Using the formula :
Area of Δ PQT / area of ΔPRS = (2/3)2
Let "A" be the area of triangle PQT.
A/(A+22) = 4/9
9A = 4(A+22)
9A-4A = 88
5A = 88
A = 88/5
A = 17.6 m2
So, area of triangle PQT is 17.6 m2.
Example 6 :
What will happen to the volume of
(a) a sphere if the radius is doubled
(b) A cylinder if the radius and the height are increased by 50% ?
Solution :
(a) Ratio of radius of old sphere and new sphere = 1 : 2
Volume of old sphere/Volume of new sphere = (1/2)3
Volume of new sphere = 8(Volume of old sphere)
(b) Radius of old cylinder = r1
Radius of new cylinder = 1.50r1
Ratio of the radius = 1 : 1.50
Volume of old cylinder / Volume of new cylinder = (1/1.50)3
Volume of new cylinder = (1.50)3 Volume of old cylinder
Volume of new cylinder = (3.375) Volume of old cylinder
So, it is multiplied by 3.375.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 150)
Apr 25, 25 11:46 AM
Digital SAT Math Problems and Solutions (Part - 150) -
AP Calculus AB Problems with Solutions (Part - 19)
Apr 24, 25 11:10 PM
AP Calculus AB Problems with Solutions (Part - 19) -
AP Calculus AB Problems with Solutions (Part - 18)
Apr 24, 25 11:06 PM
AP Calculus AB Problems with Solutions (Part - 18)
