AREA OF A SECTOR OF A CIRCLE

The ratio of the area of a sector to the area of the corresponding circle is always equal to the ratio of the central angle of the sector θ to the complete angle of the circle, that is 2π radians.

In the diagram shown below, let A be the area of the sector shown below.

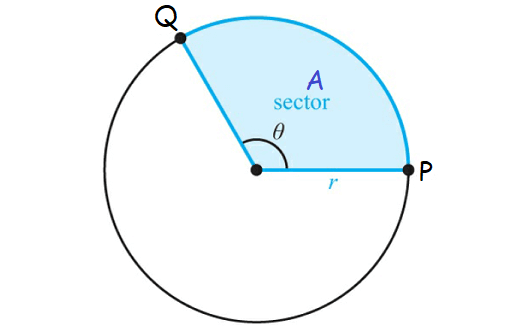
Then, we have

A/πr² = θ/π

Multiply both sides by πr².

A = (1/2)r²θ

where r is the radius of the circle and θ is the angle subtended at the center measured in radians.

Example 1 :

Find the area of the sector shaded in blue color. Angle given at the center is in radians.

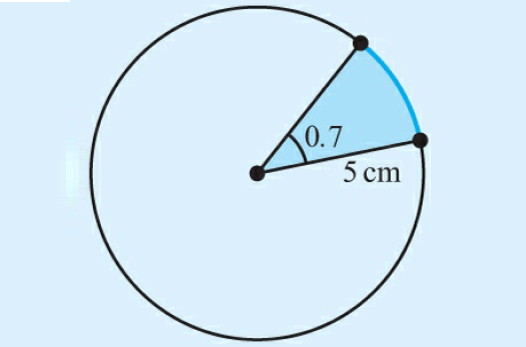
Solution :

Area of the sector :

= (1/2)r²θ

Substitute r = 5 and θ = 0.7.

= (1/2)(5)²(0.7)

= 8.75 cm²

Example 2 :

Find the area of the sector shaded in blue color. Angle given at the center is in radians.

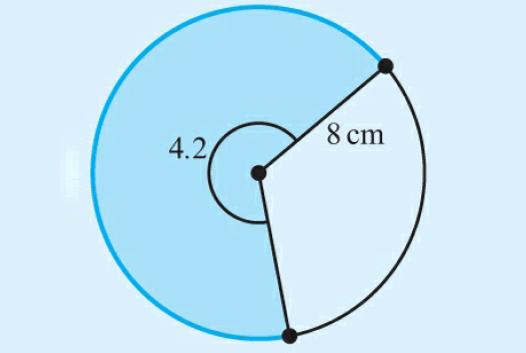
Solution :

Area of the sector :

= (1/2)r²θ

Substitute r = 8 and θ = 4.2.

= (1/2)(8)²(4.2)

= 134.4 cm²

Example 3 :

Find the area of the sector POQ.

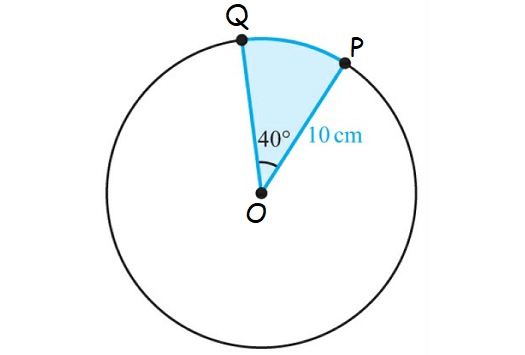
Solution :

Convert 40° to radians.

40° = 40° x (π/180°)

= 2π/9

Area of the sector :

= (1/2)r²θ

Substitute r = 10 and θ = 0.7.

= (1/2)(10)²(2π/9)

= 34.9 cm²

Example 4 :

Find the area of the sector shaded in blue color.

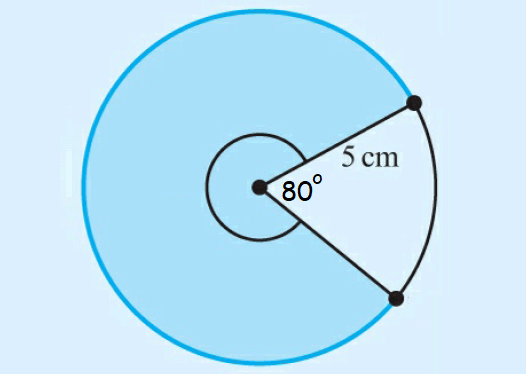
Solution :

Central angle of the shaded region :

= 360° - 80°

= 280°

Convert 280° to radians.

280° = 280° x (π/180°)

= 14π/9

Area of the sector :

= (1/2)r²θ

Substitute r = 5 and θ = 14π/9.

= (1/2)(5)²(14π/9)

= 61.09 cm²

Example 5 :

A circle has radius 7.5 cm Find the area of the sector in the circle whose central angle measures π/4 radians.

Solution :

Area of the sector :

= (1/2)r²θ

Substitute r = 7.5 cm and θ = π/4.

= (1/2)(7.5)²(π/4)

= 22.09 cm²

Example 6 :

A circle has radius 6 cm Find the area of the sector in the circle whose central angle measures 45°.

Solution :

Convert 45° to radians.

45° = 45° x (π/180°)

= π/4

Area of the sector :

= (1/2)r²θ

Substitute r = 6 and θ = π/4.

= (1/2)(6)²(π/4)

= 14.14 cm²

Example 7 :

The area of a sector is 24π cm². If the radius of the circle is 8 cm, find the central angle of the sector in radians.

Solution :

Area of the sector = 24π cm²

(1/2)r²θ = 24π

Substitute r = 8.

(1/2)(8)²θ = 24π

(1/2)(64)θ = 24π

32θ = 24π

Divide both sides by 32.

θ = 24π/32

θ = 3π/4

The central angle of the sector is 3π/4 radians.

Example 8 :

The area of a sector is 25π cm². If the radius is 10 cm, find the central angle of the sector in degrees.

Solution :

Area of the sector = 25π cm²

(1/2)r²θ = 25π

Substitute r = 10.

(1/2)(10)²θ = 25π

(1/2)(100)θ = 25π

50θ = 25π

Divide both sides by 50.

θ = π/2

Convert π/2 to degrees.

 π/2 =  (π/2) x (180°/π)

= 90°

The central angle of the sector is 90°.

Example 9 :

The area of a sector is 18.75π cm². If the central angle of the sector is π/6 radians, find the radius of the circle.

Solution :

Area of the sector = 18.75π cm²

(1/2)r²θ = 18.75π

Substitute θ = π/6.

(1/2)r²(π/6) = 18.75π

πr²/12 = 18.75π

Multiply both sides by 12.

πr² = 225π

Divide both sides by π.

r² = 225

Take square root on both sides.

r = 15

The radius of the circle is 15 cm.

Example 10 :

The area of a sector is 50 cm². If the central angle of the sector is π/4 radians, find the area of the circle.

Solution :

Area of the sector = 50 cm²

(1/2)r²θ = 50

Substitute θ = π/4.

(1/2)r²(π/4) = 50

πr²/8 = 50

Multiply both sides by 8.

πr² = 400

Area of the circle = 400 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.