AREA OF COMPOUND FIGURES

Example 1 :

Find the area of the given polygon

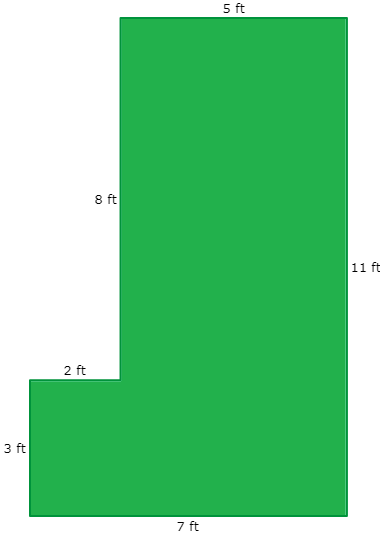
Solution :

By drawing a horizontal line (FG)  parallel to the side DC, we have divided the given polygon into two rectangles.

(i) ABFG is a rectangle

(ii) EGDC is also a rectangle

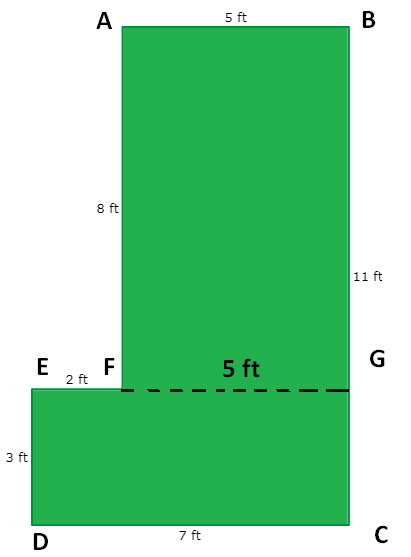
Area of ABFG :

Area of rectangle = Length x width

length (AF) = 8 ft and width AB = 5 ft

  =  8 x 5 = 40 square feet ---(1)

Area of EGDC :

length (DC) = 7 ft and width DE = 3 ft

  =  7 x 3 = 21 ft² ---(2)

(1) + (2) 

Area of given polygon

= Area of rectangle ABFG + Area of rectangle EGDC

 =  40 + 21 = 61 ft²

Example 2 :

Find the area of the given polygon

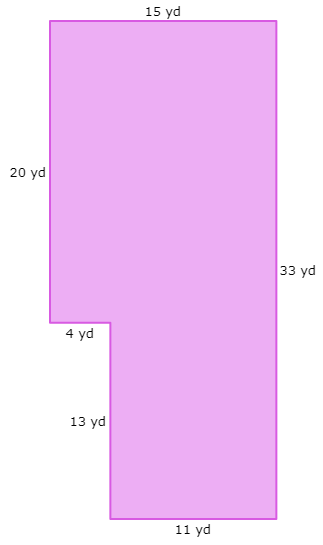
Solution :

By drawing a horizontal line (DE)  parallel to the side GF, we have divided the given polygon into two rectangles.

(i) ABCE is a rectangle

(ii) DEGF is also a rectangle

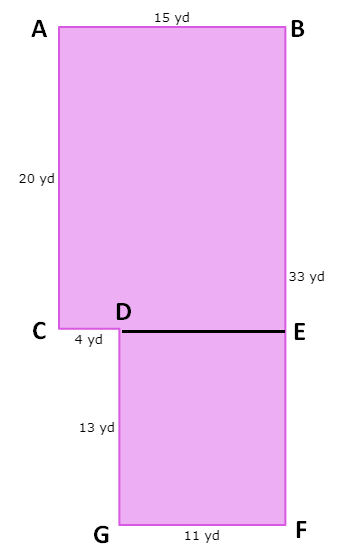
Area of rectangle ABCE :

Area of rectangle = Length x width

length (AC) = 20 yd and width AB = 15 yd

  =  20 x 15 = 300 yd² ---(1)

Area of DEGF :

length (DG) = 13 yd and width GF = 11 yd 

  =  13 x 11 = 143 yd² ---(2)

(1) + (2) 

Area of given polygon

= Area of rectangle ABCE + Area of rectangle DEGF 

 =  300 + 143 = 443 yd²

Example 3 :

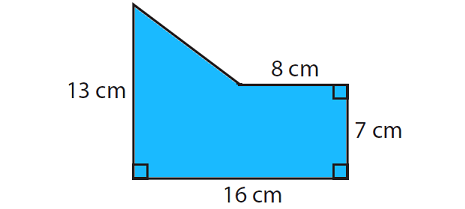
Find the area of the given polygon

Solution :

By drawing a horizontal line, we have divided the given shape as two parts.

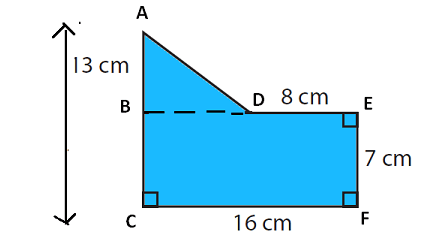
(1) BECF is a rectangle

(2) ABD is triangle

Area of the given polygon

= Area of rectangle BECF + Area of triangle ABD

Area of rectangle BECF :

length CF = 16 cm and width BC = 7 cm

= length x width 

 =  16 x 7

=  112 cm²  ----(1)

Area of triangle ABD :

Base BD  =  BE - DE  =>  16 - 8 => 8 cm

Height AB = AC - BC => 13 - 7 => 6

Area of triangle ABD = (1/2) x b x h

  =  (1/2) x 8 x 6 ==> 24 cm²----(2)

(1) + (2) 

Area of the given polygon = 112 + 24 ==> 136 cm²

Example 4 :

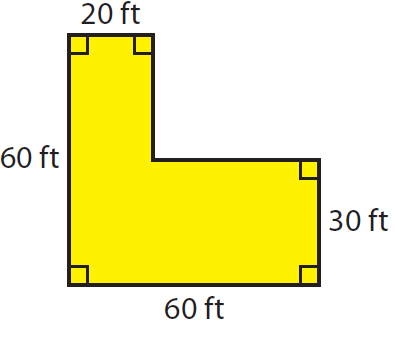
Find the area of the given polygon

Solution :

By drawing a horizontal line, we have divided the given shape as two rectangles.

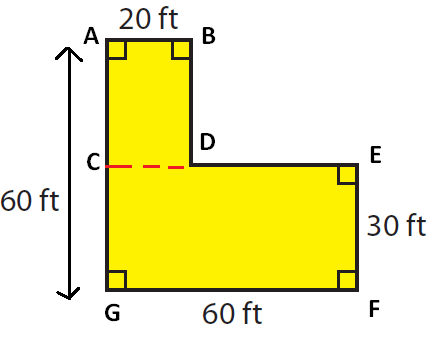
(1) ABCD is a rectangle

(2) CEFG is rectangle

Area of the given polygon

= Area of rectangle ABCD +  Area of triangle DEFG

Area of rectangle ABCD :

length AB = 20 ft and

width AC = AG - CG => 60- 30 = 30 ft

= length x width 

 =  20 x 30

=  600 ft²  ----(1)

Area of triangle DEFG :

length GF = 60 ft and

width FE = 30 ft

= length x width 

 =  60 x 30

=  1800 ft²  ----(1)

(1) + (2) 

Area of the given polygon = 600 + 1800 ==> 2400 ft²

Example 5 :

Find the area of the given polygon

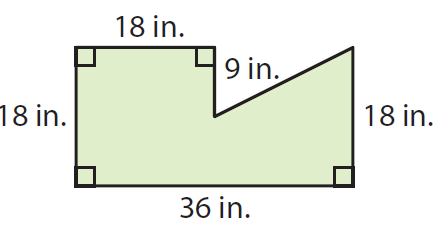
Solution :

Extend the top edge and the right edge of the polygon.

By subtracting the area of triangle BFB from the rectangle ABCD. We can find the area of the given polygon.

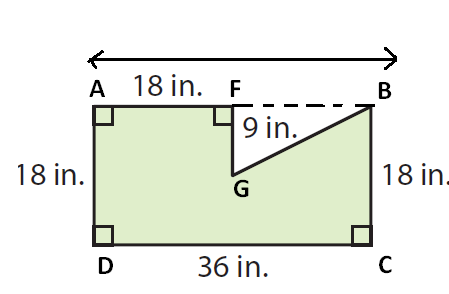
Area of the given polygon

= Area of rectangle ABCD - Area of triangle GFB

Area of rectangle ABCD :

length AD = 36 inches and

width AB = 18 inches

= length x width 

 =  36 x 18

=  648 in²  ----(1)

Area of triangle GFB :

base FG = 9 inches and

Height FB = AB - AF ==> 36 - 18 ==> 18 inches

= (1/2) x base x height

 =  (1/2) x 9 x 18

=  81 in²  ----(1)

Area of the given polygon = 648 - 81 = 567 in²

Example 6 :

Find the area of the portion of the basketball court shown.

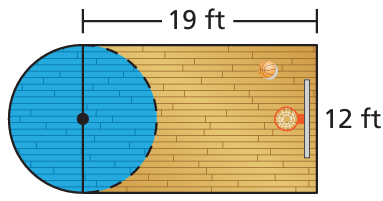
Solution :

Area of basketball court

= area of rectanlge + area of semi circle

= length x width + (1/2)πr²

length = 19 ft, width = 12 ft

diameter of semicircle = 12 ft

radius = 6 ft

= 19 x 12 + (1/2) x 3.14 x 6²

= 228 + 56.52

= 284.52 square ft

Example 7 :

In the figure below, trapezoid DEFG is made up of triangle MHK and two identical parallelograms DEHM and MKFG. The area of triangle MHK is 105 square inches. Find the area of trapezoid DEFG.

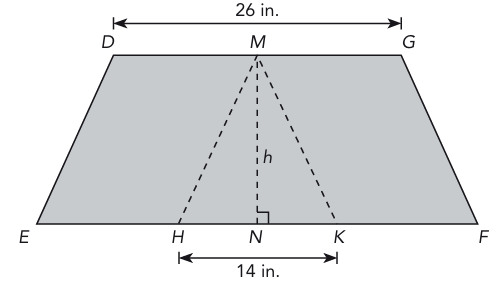
Solution :

Area of triangle = (1/2) x base x height

base of triangle = 14 inch

height = h = ?

Given that, area of triangle = 105 square inches

(1/2) x 14 x h = 105

7 h = 105

h = 105/7

h = 15 inches

DG = 26 inches

DM = 26/2

DM = 13 inches

EF = EH + HK + KF

= 13 + 14 + 13

= 40 inches

Area of trapezium = (1/2) x h (a + b)

= (1/2) x 15 x (40 + 26)

= (1/2) x 15 x 66

= 33 x 15

= 495 square inches

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.