AREA OF IRREGULAR SHAPES WORKSHEET

Problem 1 :

Find the area of the shape shown below. 

Problem 2 :

Find the area of the shape shown below. 

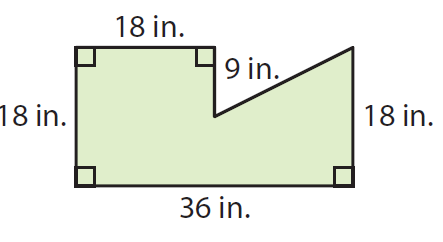
Problem 3 :

Find the area of the shape shown below. 

Detailed Answer Key

Problem 1 :

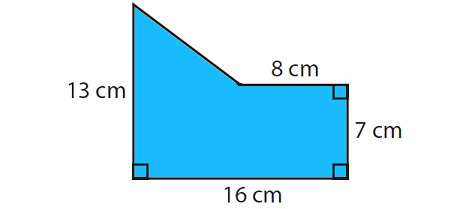
Find the area of the shape shown below. 

Solution : 

By drawing a horizontal line, we can divide the given shape into two parts (triangle and rectangle) as shown below. 

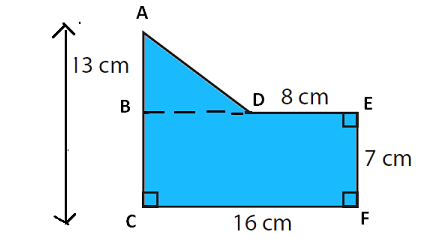
(1) BECF is a rectangle

(2) ABD is triangle

Area of the given shape :

= Area of rectangle BECF + Area of triangle ABD

Area of rectangle BECF :

length CF = 16 cm and width BC = 7 cm

= length x width 

 =  16 x 7

=  112 cm²  ----(1)

Area of triangle ABD :

Base BD  =  BE - DE ----> 16 - 8  =  8 cm.

Height AB = AC - BC ----> 13 - 7  =  6 cm.

Area of triangle ABD  =  (1/2) x b x h

  =  (1/2) x 8 x 6 ==> 24 cm²----(2)

Area of the given shape :

=  (1) + (2)

=  112 + 24

=  136 cm²

Problem 2 :

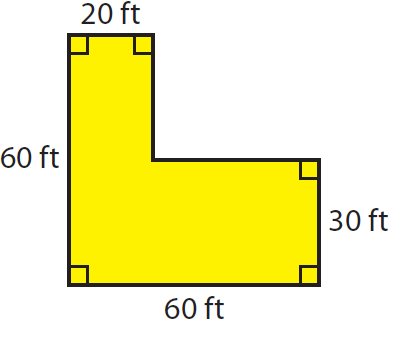
Find the area of the shape shown below. 

Solution : 

By drawing a horizontal line, we can divide the given shape into two rectangles.

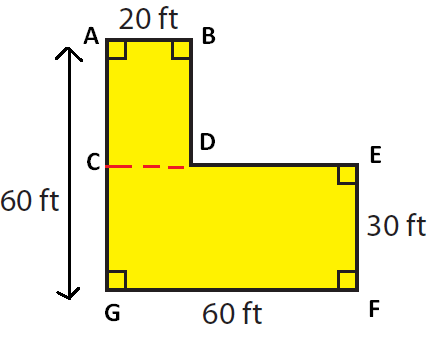
(1) ABCD is a rectangle

(2) CEFG is rectangle

Area of the given polygon

=  Area of rectangle ABCD +  Area of triangle DEFG

Area of rectangle ABCD :

length AB = 20 ft and

width AC = AG - CG ----> 60- 30 = 30 ft

= length x width 

 =  20 x 30

=  600 ft²  ----(1)

Area of triangle DEFG :

length GF = 60 ft

width FE = 30 ft

= length x width 

 =  60 x 30

=  1800 ft²  ----(1)

Area of the given shape :

=  (1) + (2)

= 600 + 1800

=  2400 ft²

Problem 3 :

Find the area of the shape shown below. 

Solution :

Extend the top edge and the right edge of the polygon.

By subtracting the area of triangle BFB from the rectangle ABCD, we can find the area of the given shape. 

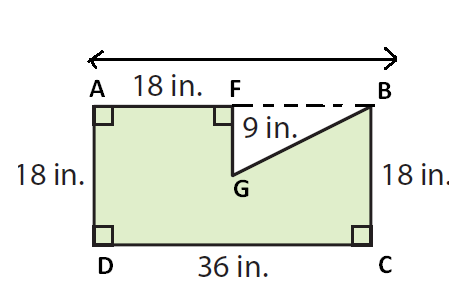
Area of the given polygon :

= Area of rectangle ABCD - Area of triangle GFB

Area of rectangle ABCD :

length AD = 36 inches and

width AB = 18 inches

= length x width 

 =  36 x 18

=  648 in²  ----(1)

Area of triangle GFB :

base FG = 9 inches and

Height FB = AB - AF ==> 36 - 18 ==> 18 inches. 

= (1/2) x base x height

 =  (1/2) x 9 x 18

=  81 in²  ----(2)

Area of the given shape :

=  (1) - (2)

=  648 - 81

=  567  in²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.