AREA OF POLYGONS

A polygon is a plane shape with straight sides. The area of a polygon measures the size of the region enclosed by the polygon. It is measured in units squared.

Area of Equilateral Triangle

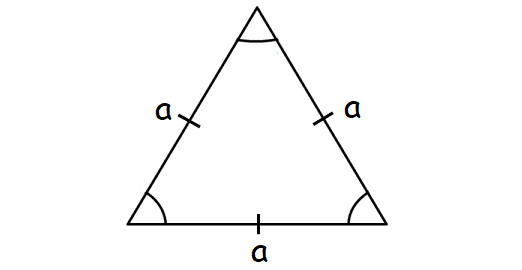
A triangle with all three sides of equal length. All the angles are 60°.

Formula for area of an equilateral triangle :

= (√3/4)a²

Area of Scalene Triangle

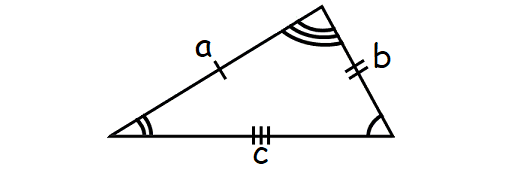
A scalene triangle is a triangle that has three unequal sides.

Formula for area of a scalene triangle :

= √s(s - a)(s - b)(s - c)

where s = (a + b + c)/2.

Area of Square

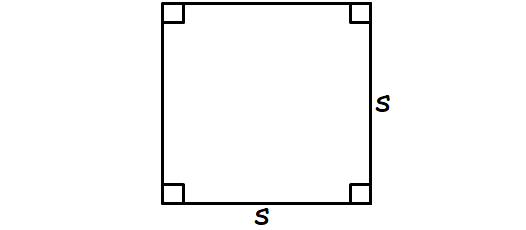
A plane figure with four equal straight sides and four right angles.

Formula for area of a square :

= s² 

Area of Rectangle

A plane figure with four straight sides and four right angles, especially one with unequal adjacent sides, in contrast to a square.

Formula for area of a rectangle :

= length x width

or

= l x w

Area of Parallelogram

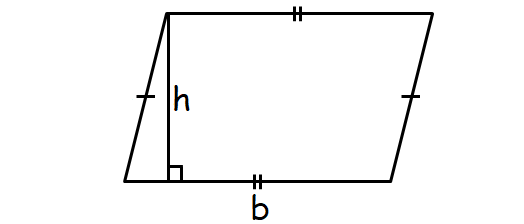
A parallelogram is a quadrilateral with opposite sides parallel.

Formula for area of a parallelogram :

= base x height

or

= b x h

Area of Rhombus

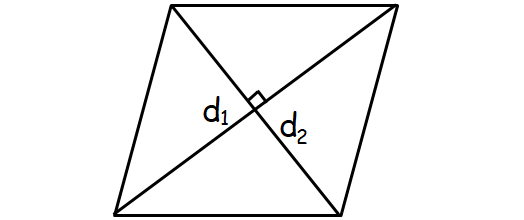
A rhombus is a parallelogram with four equal sides and equal opposite angles.

Formula for area of a rhombus :

= (1/2) x (d₁ x d₂)

Area of Quadrilateral

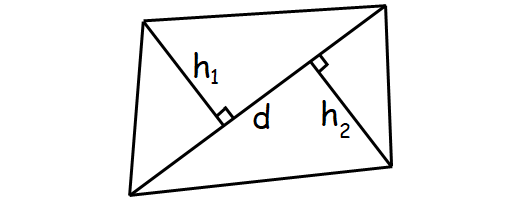
A shape which is having four sides is generally called quadrilateral.

Formula for area of a quadrilateral :

= (1/2) x d x (h₁ + h₂)

Area of Trapezoid

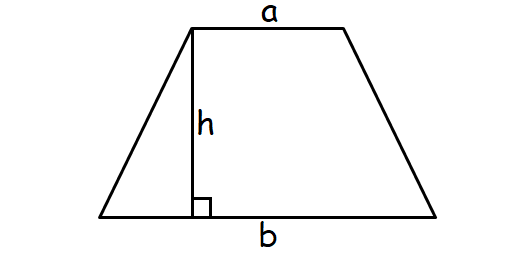
A quadrilateral with one pair of sides parallel.

Formula for area of a trapezoid :

= (1/2) x h(a + b)

Example 1 :

Find the area of the parallelogram.

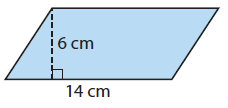
Solution :

Area of the parallelogram = b x h

Substitute b = 14 and h = 6.

  = 14 x 6

= 84 cm²

Example 2 :

What is the area of a parallelogram that has a base of 12.75 in. and a height of 2.5 in.?

Solution :

Area of the parallelogram = b x h

Substitute b = 12.75 and h = 2.5.

= 12.75 x 2.5

= 31.875 in²

Example 3 :

Find the area of trapezoid.

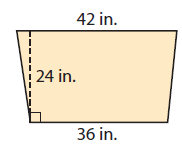
Solution :

Area of the trapezoid = (1/2) x h(a + b)

Substitute a = 42, b = 36 and h = 24.

  = (1/2) x 24(36 + 42)

= 12 x 78

= 936 in²

Example 4 :

The bases of a trapezoid are 11 meters and 14 meters. If its height is 10 meters, find the area.

Solution :

Area of the trapezoid = (1/2) x h(a + b)

Substitute a = 11, b = 14 and h = 10.

= (1/2) x 10(11 + 14)

= 5 x 25

  = 125 m²

Example 5 :

The diagonals of a rhombus are 21 m and 32 m. What is the area of the rhombus?

Solution :

Area of rhombus = (1/2) x (d₁ x d₂)

Subtract d₁ = 21 and d₂ = 32.

= (1/2) x (21 x 32)

= 21 x 16

= 336 m²

Example 6 :

Find the area of the given figure. Explain how you found your answer.

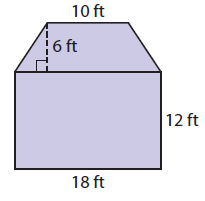
Solution :

In the given figure we can find two shapes, trapezoid and rectangle.

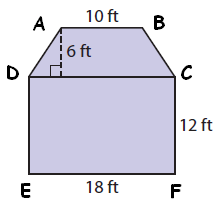
ABCD  is a trapezoid, DCEF is a rectangle.

Area of the given figure :

 =  Area of trapezoid + Area of rectangle

Area of trapezoid :

= (1/2) x h(a + b)

Substitute a = 10, b = 18 and h = 6

= (1/2) x 6(10 + 18)

= 3 x 28

= 84 ft²

Area of rectangle DCEF :

= l x w

Substitute l = 18 and w = 12.

= 18 x 12

= 216 ft²

Area of the given figure :

= 84 + 216

= 300 ft²

Example 6 :

In the diagram below, MATH is a rectangle, GB = 4.6, MH = 6, and HT = 15.

What is the area of polygon MBATH?

1) 34.5      2) 55.5      3) 90.0      4) 124.5

To find the area of the shaded region, from the area of the rectangle we should subtract area of right triangles inside the rectangle.

Using Pythagorean theorem, in triangle GBA

BA² = GB² + GA²

BA² = GB² + GA² 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.