AREA OF REGULAR POLYGON
Area of an Equilateral Triangle
The area of any triangle with base length b and height h is given by A = 1/2⋅bh. The following formula for equilateral triangles, however, uses only the side length.
Theorem :
The area of an equilateral triangle is one fourth the square of the length of the side times √3.
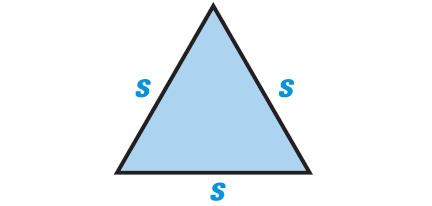
Area of the equilateral triangle shown above is
= √3/4 ⋅ s2
Proof :
Given : ΔABC is equilateral
To prove : Area of ΔABC is A = 1/4 ⋅ √3 ⋅ s2
In ΔABC, draw the altitude from B to side AC.
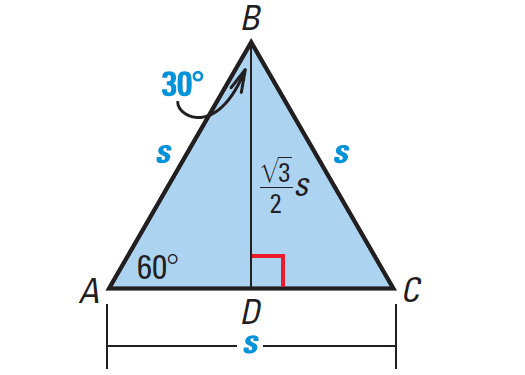
Then ΔABD is a 30°-60°-90° triangle.
To find the length of the altitude BD, use Pythagorean theorem in right ΔBDC.
So, we have
BD2 + DC2 = BC2
Substitute.
BD2 + (s/2)2 = s2
BD2 + s2/4 = s2
Subtract s2/4 from each side.
BD2 = s2 - s2/4
Simplify.
BD2 = 3s2/4
Take square root on each side.
BD = √3s/2
Using the formula for the area of a triangle.
A = 1/2 ⋅ bh
Substitute.
A = 1/2 ⋅ s(√3s/2)
A = √3/4 ⋅ s2
Area of a Regular Polygon
Theorem :
The area of a regular n-gon with side length s is half the product of the apothem a and the perimeter P.
So,
A = 1/2 ⋅ aP
or
A = 1/2 ⋅ a ⋅ (ns)
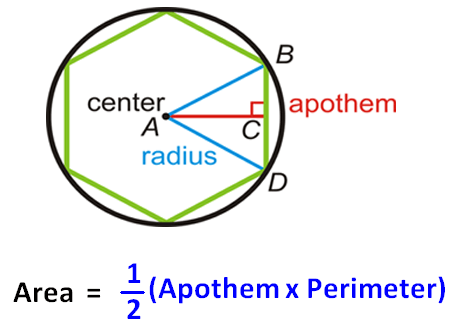
Proof :
Think of the hexagon ABCDEF as inscribed in a circle.
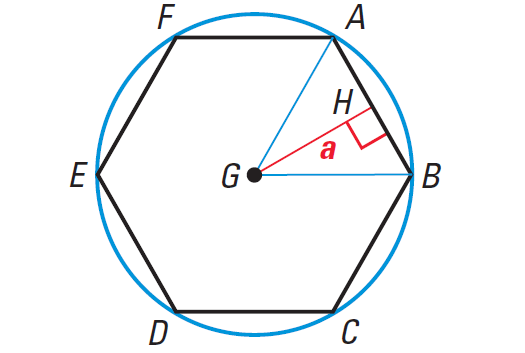
The center of the polygon and radius of the polygon are the center and radius of its circumscribed circle, respectively.
The distance from the center to any side of the polygon is called the apothem of the polygon. The apothem is the height of a triangle between the center and two consecutive vertices of the polygon.
We can find the area of any regular n-gon by dividing the polygon into congruent triangles.
A = area of one triangle ⋅ number of triangles
A = (1/2 ⋅ apothem ⋅ side length s) ⋅ number of sides
A = 1/2 ⋅ apothem ⋅ (number of sides ⋅ side length s)
A = 1/2 ⋅ apothem ⋅ perimeter of polygon
This approach can be used to find the area of any regular polygon.
Central Angle of a Regular Polygon
A central angle of a regular polygon is an angle whose vertex is the center and whose sides contain two consecutive vertices of the polygon. We can divide 360° by the number of sides to find the measure of each central angle of the polygon.
Finding the Area of an Equilateral Triangle
Example 1 :
Find the area of an equilateral triangle with side length 4 inches.
Solution :
The formula for area of an equilateral triangle is given by
A = √3/4 ⋅ s2
Substitute s = 4.
A = √3/4 ⋅ 42
Simplify.
= √3/4 ⋅ 16
= √3 ⋅ 4
= 4√3
So, the area of the equilateral triangle is 4√3 square inches.
Finding the Area of a Regular Polygon
Example 2 :
Find the area of the regular pentagon shown below.
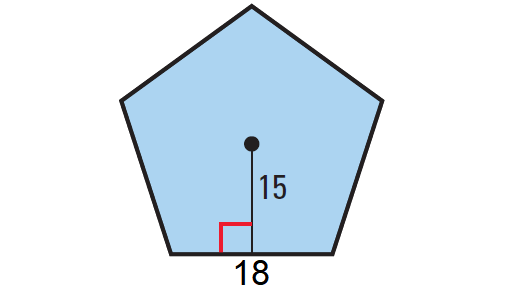
Solution :
To find area of any regular polygon, we need to know the length of apothem and perimeter.
In the above regular pentagon,
Apothem = 15 units
Pentagon has 5 sides. So, the perimeter is
P = side length ⋅ no. of sides
= 18 ⋅ 5
= 90 units
The formula for area of a n-gon is given by
A = 1/2 ⋅ apothem ⋅ perimeter of polygon
Substitute.
= 1/2 ⋅ 15 ⋅ 90
Simplify.
= 675
So, the area of the regular pentagon is 675 square units.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

