AREA OF RHOMBUS

The area of a rhombus is equal to one half the product of the lengths of the diagonals.  

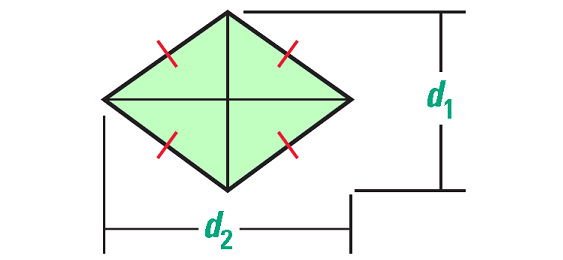
Let d₁ and d₂ be the lengths of diagonals of a rhombus. 

Example 1 :

If the lengths of the diagonals of a rhombus are  16 cm and 30 cm, find its area.

Solution :

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 16 for d₁ and 30 for d₂.

=   1/2 ⋅ (16 ⋅ 30)

=   8 ⋅ 30

=  240 cm²

So, area of the rhombus is 240 square cm.

Example 2 :

Find the area of the rhombus shown below. 

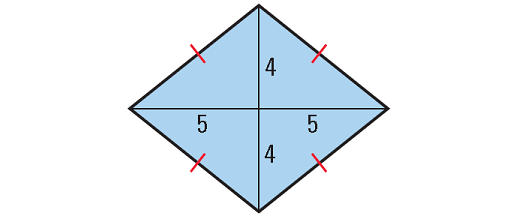
Solution :

In the rhombus shown above,

d₁  =  5 + 5  =  10 units

d₂  =  4 + 4  =  8 units

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 10 for d₁ and 8 for d₂.

=   1/2 ⋅ (10 ⋅ 8)

=   5 ⋅ 8

=  40

So, area of the rhombus is 40 square units.

Example 3 :

Area of a rhombus is 192 square cm. If the length of one of the diagonals is 16 cm, find the length of the other diagonal. 

Solution :

Area of the rhombus  =  192 cm²

1/2 ⋅ (d₁d₂)  =  192

Substitute 16 for d₁.

1/2 ⋅ (16 ⋅ d₂)  =  192

8 ⋅ d₂  =  192

Divide each side by 8.

d₂  =  24 cm

So, the length of the other diagonal is 24 cm. 

Example 4 :

Area of a rhombus is 120 square units. If the lengths of the diagonals are 10 units and (7x + 3) units, then find the value of x.  

Solution :

Area of the rhombus  =  120 cm²

1/2 ⋅ (d₁d₂)  =  120

Substitute 10 for d₁ and (7x + 3) for d₂. 

1/2 ⋅ [10(7x + 3)]  =  120

5(7x + 3)  =  120

Divide each side by 5. 

7x + 3  =  24

Subtract 3 from each side. 

7x  =  21

Divide each side by 7.

x  =  3

Example 5 :

Area of the rhombus shown below is 48 square inches. What is the value of x ? 

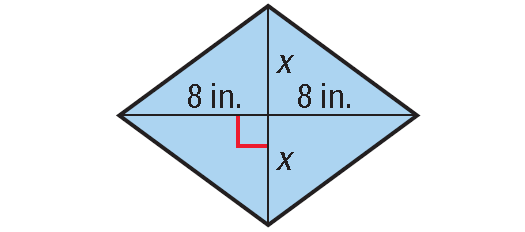
Solution :

In the rhombus shown above,

d₁  =  8 + 8  =  16 units

d₂  =  x + x  =  2x units

Given : Area of the rhombus is 48 square inches. 

Then, 

1/2 ⋅ (d₁d₂)  =  48

Substitute 16 for d₁ and 2x for d₂.

1/2 ⋅ (16 ⋅ 2x)  =  48

8 ⋅ 2x  =  48

16x  =  48

Divide each side by 16.

x  =  3

Example 6 :

Find the area of the rhombus shown below. 

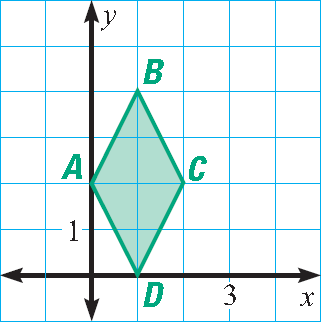
Solution :

Measure the lengths of the diagonals AC and BD.  

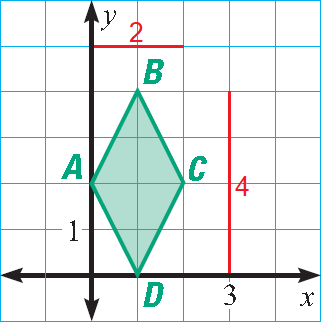
The lengths of the diagonals are  4 units and 2 units. 

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 4 for d₁ and 2 for d₂.

=   1/2 ⋅ (4 ⋅ 2)

=   2 ⋅ 2

=  4 

So, area of the rhombus is 4 square units.

Example 7 :

Find the area of the rhombus having each side equal to 17 cm and one of its diagonals equal to 16 cm.

Solution :

Let A, B, C and D be the vertices of the rhombus. 

The diagonals of a rhombus will be perpendicular and they will bisect each other. 

Then, we have

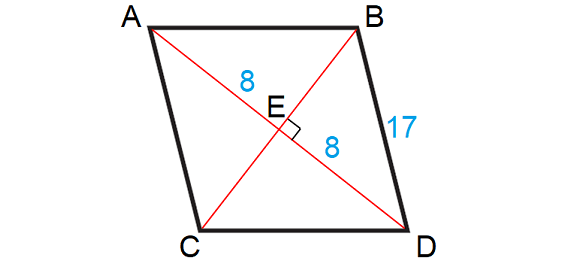
In the above rhombus, consider the right angled triangle BDE. 

By Pythagorean Theorem, 

BD²  =  BE² + DE²

17²  =  BE² + 8²

289  =  BE² + 64

Subtract 64 from each side. 

225  =  BE²

15²  =  BE²

15  =  BE

Then, 

EC  =  15

Length of the diagonal BC : 

BC  =  BE + EC

BC  =  15 + 15

BC  =  30 units

So, the lengths of the diagonals are 16 units and 30 units. 

Formula for area of a rhombus :

=   1/2 ⋅ (d₁d₂)

Substitute 16 for d₁ and 30 for d₂.

=   1/2 ⋅ (16 ⋅ 30)

=   8 ⋅ 30

=  240 

So, area of the rhombus is 240 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.