AREA OF RIGHT TRIANGLE PRACTICE QUESTIONS

A right triangle is a triangle with one of the angles as 90 degrees. A 90 degree angle is called a right angle, and hence the triangle with a right angle is called a right triangle.

Area of right triangle  =  (1/2) ⋅ base ⋅ height

Find the area of triangles given below :

Question 1 :

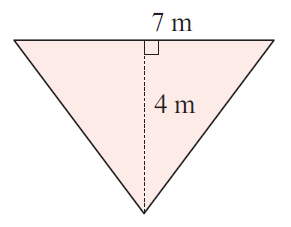
Solution :

Base  =  7 m and height  =  4 m

Area triangle  =  (1/2) ⋅ 7 ⋅ 4

=  14 m²

So, area of the given triangle is 14 m².

Question 2 :

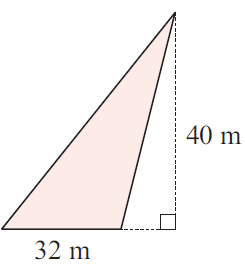
Solution :

Base  =  32 m and height  =  40 m

Area triangle  =  (1/2) ⋅ 32 ⋅ 40

=  640 m²

So, area of the given triangle is 640 m².

Question 3 :

A right angled triangle has sides of length 3 m, 4 m and 5 m.

a) Find the area of the triangle ABC.

b) A perpendicular is drawn from side [AC] to B Let this perpendicular have length x m. Find x.

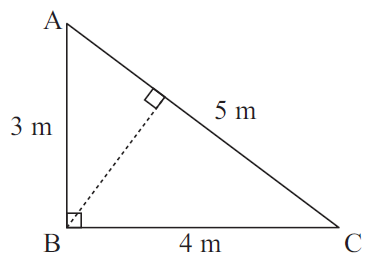
Solution :

Area of triangle ABC  =   (1/2) ⋅ Base ⋅ height  ----(1)

Here if BC  =  base and height  =  AB.

Note :

If AC is base and the perpendicular drawn from B is known as height.

From (1)

Area of triangle ABC  =   (1/2) ⋅ BC ⋅ AB ----(1)

Area of triangle ABC  =   (1/2) ⋅ AC ⋅ x ----(2)

(1)  =  (2)

(1/2) ⋅ BC ⋅ AB  =  (1/2) ⋅ AC ⋅ x

4 ⋅ 3  =  5 ⋅ x

x  =  12/5

x  =  2.4 m

Question 4 :

The area of a triangle with base b and height h is given

by the formula A  =  (1/2) bh

Find:

a) the base if the area is 84 cm² and the height is 12 cm

b) the height if the area is 1 m² and the base is 2 m.

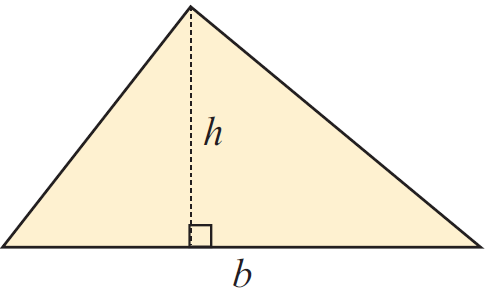
Solution :

Let  A  =  (1/2) bh  ---(1)

a) the base if the area is 84 cm² and the height is 12 cm

Given : 

A  =  84 cm² and h  =  12 cm

By applying these values in (1), we get

84  =  (1/2) bh

84  =  (1/2) ⋅ b ⋅ (12)

84  =  6b

b  =  84/6

b  =  14

Question 5 :

Find area of the following figure ABC.

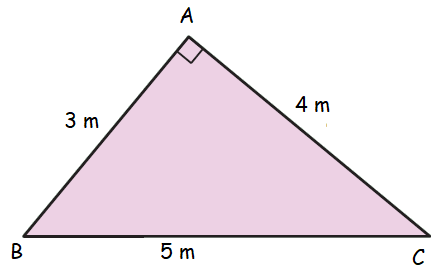
Solution :

In the triangle ABC, BC is the base and AC is height.

BC  =  5 m and AC  =  4 m

Area of triangle  =  (1/2) 5 ⋅ 4

=  10 m²

Question 6 :

Area of the picture given below.

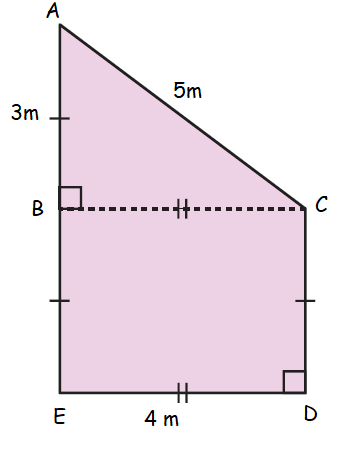
Solution :

Area of triangle ABC  =  (1/2) ⋅ BC ⋅ AB

=  (1/2) ⋅ 4 ⋅ 3

=  6 m²   ----(1)

Area of rectangle BCDE  =  length x width

=  4(3)

=  12 m²   ----(2)

(1) + (2)

Area of the given picture  =  6 + 12

=  18 m²

So, area of the given picture is 18 m²

Question 7 :

The hypotenuse of a right triangle is 17 cm long. If one of the remaining two sides is 8 cm in length, then the length of the other side is:

(a) 15 cm    (b) 12 cm    (c) 13 cm    (d) none of these

Solution :

Let x be the length of the other side of the right triangle

Hypotenuse = 17 cm

One side = 8 cm

Since it is right triangle, it should satisfy Pythagorean theorem.

8² + x² = 17²

x² = 289 - 64

x² = 225

x = 15

So, the required length of the other side is 15 cm.

Question 8 :

Shown is a square garden with a triangular pond. Find the area of the garden that is

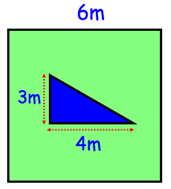
Solution :

Area of garden = Area of square - area of triangle

= 6 x 6 - (1/2) x 4 x 3

= 36 - 6

= 30 m²

Question 9 :

Shown is a triangular brick wall with a rectangular window. Find the area of the wall that is

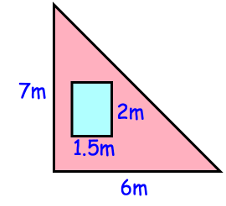
Solution :

Area of triangular brick = Area of triangle - area of rectangle

= (1/2) x 6 x 7 - 1.5 x 2

= 3 x 7 - 3

= 21 - 3

= 18 m²

Question 10 :

Shown is a pattern that is made from a rectangle and a triangle. Find the area of the pattern

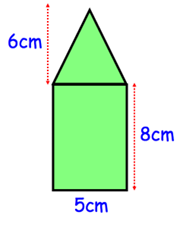
Solution :

Area of the figure shown = Area of rectangle + area of triangle.

= 5 x 8 + (1/2) x 5 x 6

= 40 + 15

= 55 cm²

Question 11 :

Shown below is a triangular field. Each chicken requires 3m². How many chickens can be kept in this field?

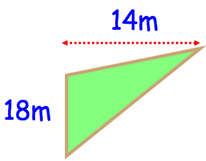
Solution :

Area of triangle = (1/2) x base x height

base = 18 m and height = 14 m

= (1/2) x 18 x 14

= 126 m²

Area of the triangle is 126 m².

Question 12 :

Many basaltic columns are hexagonal. The top of one of these columns is a regular hexagon as shown below. Find its area

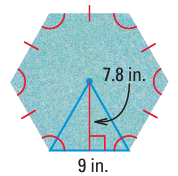
Solution :

Area of hexagon = 6(Area of triangle)

= 6(1/2) x 9 x 7.8

= 3 x 9 x 7.8

= 210.6 square inches

Area of the hexagon above is 210.6 square inches.

Question 13 :

Given that the area of the triangle is 99 square meters, what is the height of the triangle?

 A) 4.5 m     B) 9 m   C) 11 m   D) 22 m

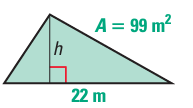
Solution :

Area of hexagon = 99 m²

(1/2) x 22 x h = 99

11 x h = 99

h = 99/11

h = 9 m

So, the required height is 9 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.