AREA OF SECTOR OF A CIRCLE

Sector is the region bounded by the bounding radii and the arc of the sector.

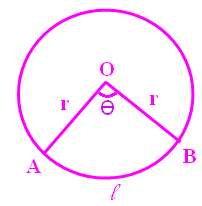
We have two formulas to find the area of sector of a circle. 

When we know the radius r of the circle and central angle θ of the sector : 

Area of the sector  =  (θ/360°) ⋅ πr²

When we know the radius r of the circle and arc length l: 

Area of the sector = (l ⋅ r) / 2

Example 1 :

Find the area of the sector whose radius and central angle are 42 cm and 60° respectively. (Take π = 3.14 and round your answer to one decimal place, if necessary)

Solution :

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Plug r  =  42, θ  =  60° and π  ≈  3.14

≈  (60° / 360°) ⋅ 3.14 ⋅ 42²

≈  923. 2

So, the area of the sector is about 923.2 cm².

Example 2 :

Find the area of the sector that is outlined with the bold line. (Take π = 3.14 and round your answer to one decimal place, if necessary)

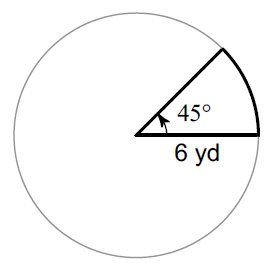
Solution :

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Plug r  =  6, θ  =  45° and π  ≈  3.14

≈  (45° / 360°) ⋅ 3.14 ⋅ 6²

≈  14.1

So, the area of the given sector is about 14.1 yd².

Example 3 :

Find the area of the sector that is outlined with the bold line. (Take π = 3.14 and round your answer to one decimal place, if necessary)

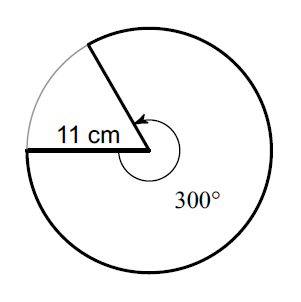
Solution :

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Plug r  =  11, θ  =  300° and π  ≈  3.14

≈  (300° / 360°) ⋅ 3.14 ⋅ 11²

≈  316.7

So, the area of the given sector is about 316.7 cm².

Example 4 :

In the diagram given below, LMN is a central angle and m∠LMN  =  78° and radius is 4 cm. find the area of sector LMN. (Take π = 3.14 and round your answer to one decimal place, if necessary)

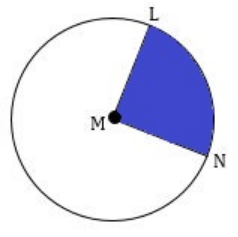
Solution :

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Plug r  =  4, θ  =  78° and Π  ≈  3.14

≈  (78° / 360°) ⋅ 3.14 ⋅ 4²

≈  10.9

So, the area of sector LMN is about 10.9 cm².

Example 5 :

In circle C, if XCZ is a central angle and XYZ is an inscribed angle and m∠XYZ  =  58° and radius is 10 inches. Find the area of sector XCZ. (Take π = 3.14 and round your answer to one decimal place, if necessary)

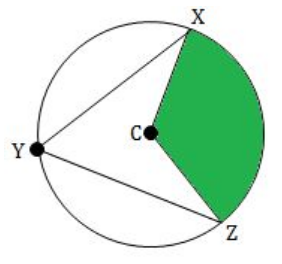
Solution :

By Inscribed Angle Theorem, we have

1/2 ⋅ m∠XCZ  =  m∠XYZ

Multiply both sides by 2.

m∠XCZ  =  2 ⋅ m∠XYZ

Given : m∠XYZ  =  58°.

Then, we have

m∠XCZ  =  2 ⋅ 58°

m∠XCZ  =  116°

So, the central angle θ is 116°.

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Plug r  =  10, θ  =  116° and Π  ≈  3.14

≈  (116° / 360°) ⋅ 3.14 ⋅ 10²

≈  101.2

So, the area of sector XCZ is about 101.2 in².

Example 6 :

If QRS is a central angle and m∠QRS = 46°, m∠SRT = 80°, and diameter is 4 inches, then find the area of the shaded sector. (Take π = 3.14 and round your answer to one decimal place, if necessary)

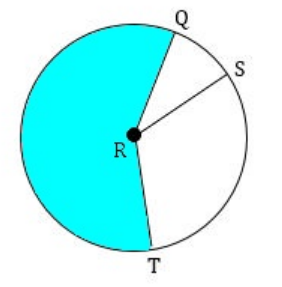
Solution :

Given : m∠QRS  =  46° and m∠SRT  =  80°.

Then, we have

m∠QRS + m∠SRT  =  46° + 80°

m∠QRS + m∠SRT  =  126°

Measure of central angle of the shaded region :

m∠QRT  =  360° - 126°

m∠QRT  =  234°

Radius of the circle :

Radius  =  Diameter / 2

Radius  =  4 / 2

Radius  =  2 inches

The formula to find area of the sector is

=  (θ / 360°) ⋅ πr²

Plug r  =  2, θ  =  234° and Π  ≈  3.14

≈  (234° / 360°) ⋅ 3.14 ⋅ 2²

≈  8.2

So, the area of the shaded sector is about 8.2 in².

Example 7 :

If the sector area of a sector intersecting Arc AB is 37 square cm and the radius is 11, then find the measure of Arc AB. (Take π = 3.14 and round your answer to the nearest whole number)

Solution :

Given : A sector is intersecting Arc AB. 

Because the given sector is intersecting Arc AB, the measure of Arc AB is nothing but the central angle of the given sector. 

Given : Area of the sector is 37 square cm. 

Then, we have

(θ / 360°) ⋅ πr²  =  37

Plug r  =  11 and π  ≈  3.14

(θ / 360°) ⋅ 3.14 ⋅ 11²  =  37

(θ / 360°) ⋅ 3.14 ⋅ 11²  =  37

(θ / 360°) ⋅ 379.94  =  37

Divide both sides by 379.94

(θ / 360°)  =  37 / 379.94

(θ / 360°)  =  0.09738

Multiply both sides by 360°.

θ  =  0.09738 ⋅ 360°

θ  ≈  35

So, the measure of Arc AB is about 35°. 

Example 8 :

Find the area of the sector and the central angle formed by the sector whose radius is 21 cm and length of arc is 66 cm. (Take π = 3.14 and round your answer to the nearest whole number)

Solution :

The formula to find area of the sector is 

=  (l ⋅ r) / 2    

Plug l  =  66 and r  =  21.

=  (66 ⋅ 21) / 2

=  693

So, the area of the sector is 693 cm².

Central angle formed by the sector :

Area of the sector  =  693

(θ / 360°) ⋅ πr²  =  693

(θ / 360°) ⋅ 3.14 ⋅ 21²  =  693

(θ / 360°) ⋅ 1384.74  =  693

Multiply both sides by 1384.74 / 360°.

θ  ⋅ (360° / 1384.74)

θ  ≈  180°

So, the area of the sector is 693 square cm and the measure of central angle is 180°.

Example 9 :

Find the area of the sector whose radius is 35 cm and perimeter is 147 cm.

Solution :

Formula to find perimeter of a sector : 

Perimeter  =  length of the arc +  2 ⋅ radius

or

P  =  l + 2r

Given : Perimeter of the sector is 147 cm and the radius is 35 cm.

Then, we have

l + 2 ⋅ 35  =  147

l + 70  =  147

Subtract 70 from both sides.

l  =  77

The formula to find area of the sector is 

=  (l ⋅ r) / 2   

Plug l  =  77 and r  =  35

=  (77 ⋅ 35) / 2

=  1347.5

So, the area of the sector is 1347.5 cm².

Example 10 :

If the sector area of a sector intersecting Arc AB is 43 square cm and the measure of Arc AB is 43°, then find the radius. (Take π = 3.14 and round your answer to one decimal place, if necessary)

Solution :

Given : The measure of Arc AB is 43°. 

Because the given sector is intersecting Arc AB, the measure of Arc AB is nothing but the central angle of the given sector. 

Then, the measure of central angle of the sector is 43°.

Given : Area of the sector is 37 square cm. 

Then, we have

(θ / 360°) ⋅ πr²  =  43

Plug θ  =  43° and π  ≈  3.14

(43° / 360°) ⋅ 3.14 ⋅ r²  =  43

Divide both sides by 3.14

(43° / 360°) ⋅ r²  =  43 / 3.14

0.1194 ⋅ r²  =  13.6943

r²  =  13.6943 / 0.1194

r²  =  11.7834 / 0.1194

r²  =  114.6926

r  ≈  10.7

So, the radius is about 10.7 cm. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.