AREA OF SHADED REGION

Example 1 :

Find the area of the shaded portion

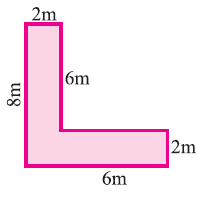
Solution :

To find the area of shaded portion of given composite figure, first let us draw a line

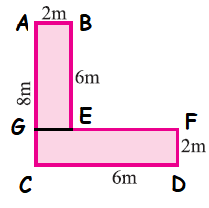
Area of given figure  =  Area of ABGE + Area of GCFD

Area of ABGE :

Area of rectangle  =  Length ⋅ Width 

length BE  =  6 m, width GE  =  2 m

Area of ABGE  =  6(2)  =  12 m²

Area of GCFD :

Area of rectangle  =  Length ⋅ Width 

length CD  =  6 m, width FD  =  2 m

Area of GCFD  =  6(2)  =  12 m²

Area of shaded portion  =  12 + 12  =  24 m²

Example 2 :

Find the area of the shaded portion

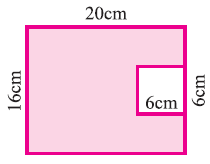
Solution :

To find the area of shaded portion, we have to subtract area of GEHF from area of rectangle ABCD.

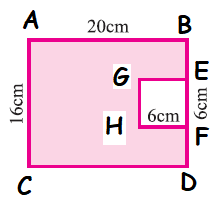
Area of shaded portion

=  Area of rectangle ABCD - Area of square GEHF

Area of ABCD :

Area of rectangle  =  Length ⋅ Width 

Length AB  =  20 cm

Width AC  =  16 cm

Area of ABCD  =  20 (16)  =  320 cm²

Area of GEHF :

Area of square (GEHF)  =  side ⋅ side

Length GE  =  6 cm

Area of square GEHF  =  6 ⋅ 6

Area of square (GEHF)  =  36 cm²

Area of shaded region  =  320 - 36  =  284 cm²

Example 3 :

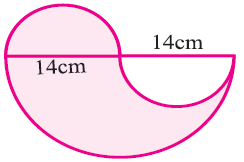
Find the area of the shaded portion

Solution :

To find the area of shaded region, we have to subtract area of semicircle with diameter CB from area of semicircle with diameter AB and add the area of semicircle of diameter AC.

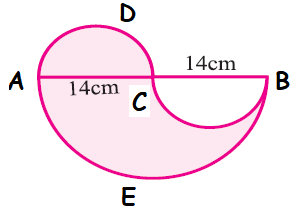
Area of shaded portion  

=  Area of AEB - Area of semicircle with diameter BC + area of semicircle with diameter AC

Area of semicircle AEB  =  (1/2) Πr²

 =  (1/2) ⋅ (22/7) ⋅ (14)²

=  (1/2) ⋅ (22/7) ⋅ 14 ⋅ 14

=  22 ⋅ 14

=  308 cm²

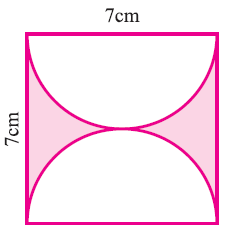
Example 4 :

Find the area of the shaded region

Solution :

To find the area of shaded portion, we have to subtract area of semicircles of diameter AB and CD from the area of square ABCD.

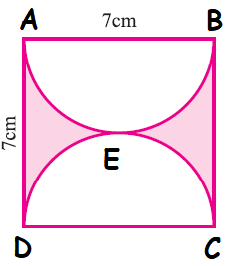
Area of shaded portion

=  Area of square ABCD - (Area of semicircle AEB + Area of semicircle DEC)

=  a² - [ (1/2) Πr²) + ((1/2) Πr²) ]

=  7² - Πr²

=  49 -  (22/7) ⋅ (7/2)²

=  49 -  (22/7) ⋅ (7/2) ⋅ (7/2)

=  49  -  38.5

=  10.5 cm²

Example 5 :

Find the area of the shaded region to the nearest 10th

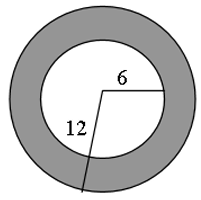
Solution :

Area of shaded region  =  Area of circle - Area of triangle

Area of circle  =  πr²

Let R be the radius of larger circle and r be the radius of smaller circle.

= πR² -  πr²

Factoring π, we get

= 3.14[12² -  6²]

= 3.14(144 - 36)

= 3.14(108)

= 339.12 square units

Example 6 :

Find the area of the shaded region to the nearest whole number :

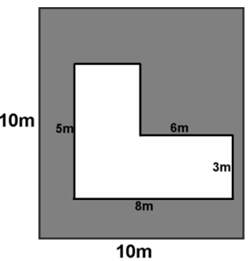
Solution :

Area of shaded region = Area of square - area of L shape

= side² - area of L shape ----(1)

Side length of square = 10 m

By drawing the horizontal line, we get the shapes square and rectangle.

= 2 x 2 + (8 x 3)

= 4 + 24

= 28 m²

Applying the value in (1), we get

= 10² - 28

= 100 - 28

= 72 square units.

Example 7 :

Find the area of the shaded region.

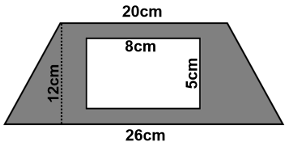
Solution :

Area of shaded region = Area of trapezium - area of rectangle

Area of trapezium = (1/2) x h (a + b)

= (1/2) x 12 x (26 + 20)

= 6(46)

= 276 square units.

Area of rectangle = length x width

= 8 x 5

= 40 square units

Area of shaded region = 276 - 40

= 236 square units.

Example 8 :

Determine the area of the shaded region.

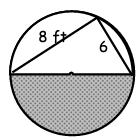
Solution :

Area of shaded region = Area of semicircle

Angle in a semicircle is right angle, diameter of the circle is hypotenuse.

Let x be the hypotenuse.

x² = 8² + 6²

x² = 64 + 36

= 100

x = 10

diameter of the circle = 10 cm

radius = 5 cm

Area of semi circle = (1/2) πr²

= (1/2) x 3.14(5)²

= 1.57(25)

= 39.25 cm²

Example 9 :

Find the area of the shaded region to the nearest 10th of a centimeter:

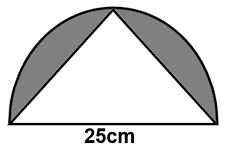
Solution :

Area of shaded region = Area of semicircle - area of triangle.

Diameter of the circle = base = 25 cm

height of the triangle = radius = 12.5 cm

= (1/2) πr² - (1/2) x base x height

= (1/2) x 3.14 x (12.5)² - (1/2) x 12.5 x 25

= 1.57 x 156.25 - 156.25

= 245.31 - 156.25

= 89.06 cm²

Example 10 :

Find the area of the shaded region to the nearest 100th of a centimeter:

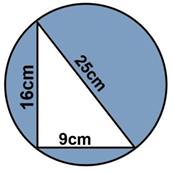
Solution :

Area of shaded region = area of circle - area of right triangle

=  πr² - (1/2) x base x height

Diameter of the circle = 25 cm, radius = 12.5 cm

= 3.14(12.5)² - (1/2) x 9 x 16

= 490.625 -72

= 418.625 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.