AREA OF TRIANGLE IN COORDINATE GEOMETRY

In Geometry, a triangle is the 3 – sided polygon which has 3 edges and 3 vertices.

Area of the triangle is a measure of the space covered by the triangle in the two-dimensional plane.

In this article, you will learn how to find the area of a triangle in the coordinate geometry.

Finding Area of a Triangle Using Coordinates :

When we have vertices of the triangle and we need to find the area of the triangle, we can use the following steps.

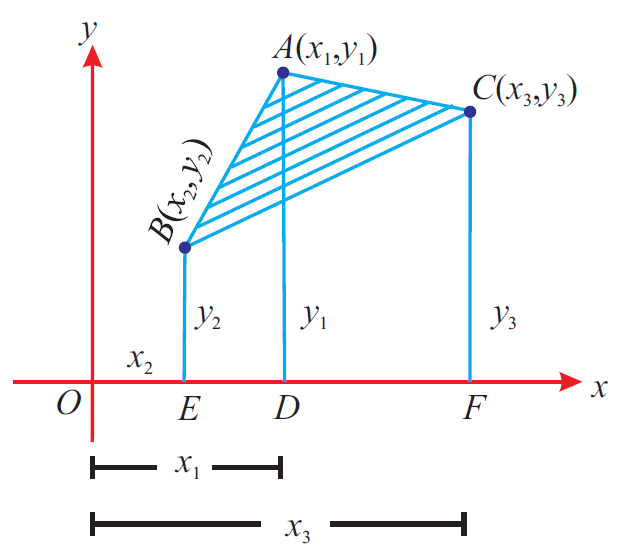
(i) Plot the points in a rough diagram.

(ii) Take the vertices in counter clock-wise direction. Otherwise the formula gives a negative value.

(iii)  Use the formula given below

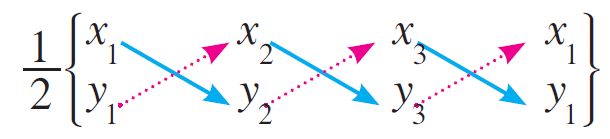
And the diagonal products x₁y₂, x₂y₃ and x₃y₁ as shown in the dark arrows. 

Also add the diagonal products x₂y₁, x₃y₂ and x₁y₃ as shown in the dotted arrows.

Now, subtract the latter product from the former product to get area of the triangle ABC.

So, area of the triangle ABC is

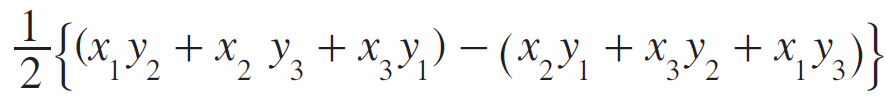
Solved Problems

Problem 1 :

Find the area of triangle whose vertices are (6, 7), (2, -9) and (-4, 1).

Solution :

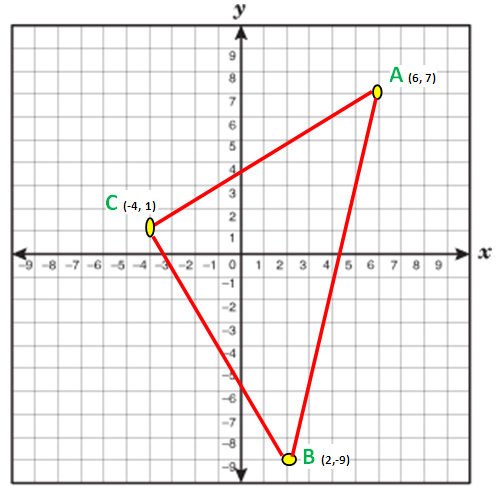
Now we have to take anticlockwise direction. So, we have to take the points in the order A (6,7) C (-4,1) and B (2,-9)

x₁ = 6     x₂ = -4      x₃ = 2

y₁ = 7     y₂ = 1       y₃ = -9

Area of the triangle ACB 

  =  (1/2) {(6 + 36 + 14) - (-28 + 2 - 54)}

  =  (1/2) {56 - ( -82 + 2)}

  =  (1/2) {56 - (-80) }

  =  (1/2) {56 + 80)}

  =  (1/2)  x 136 

  =  68 Square units.

So, the area of triangle ACB is  68 square units.

Problem 2 :

Find the area of triangle whose vertices are (3, 4), (2, -1) and (4, -6).

Solution :

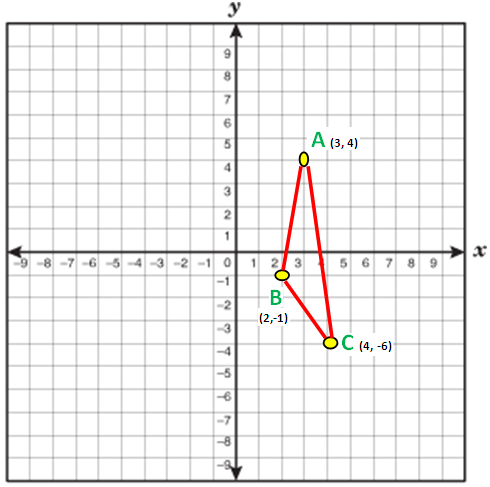
Now we have to take anticlockwise direction. So, we have to take the points in the order A (6,7) C (-4,1) and B (2,-9)

x₁ = 3     x₂ = 2         x₃ = 4

y₁ = 4     y₂ = -1        y₃ = -6

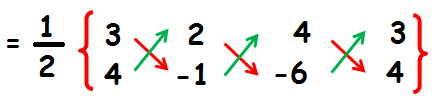
Area of the triangle ACB 

  =  (1/2) {(-3 - 12 + 16) - (8 - 4 - 18)}

  =  (1/2) {(-15 + 16) - (8 - 22)}

  =  (1/2) {1 - (-14) }

  =  (1/2) x (1 + 14)

  =  (1/2)  x 15 

=  15/2

=  7.5

So, the area of triangle ABC is 7.5 square units.

Problem 3 :

Find the area of triangle whose vertices are (5, 6), (2, 4) and (1, -3).

Solution :

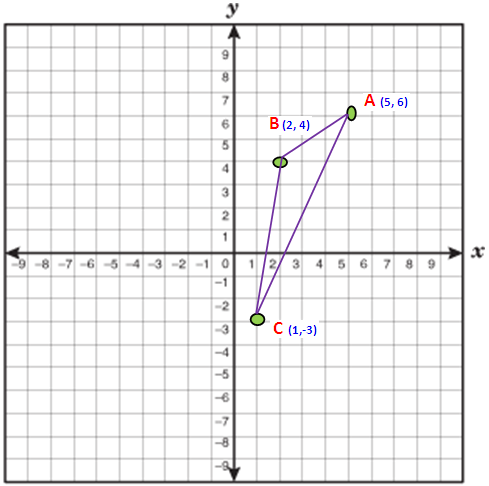
Now we have to take anticlockwise direction. So we have to take the points in the order A (5,6) B (2,4) and C (1,-3)

x₁ = 5     x₂ = 2        x₃ = 1

y₁ = 6     y₂ = 4       y₃ = -3

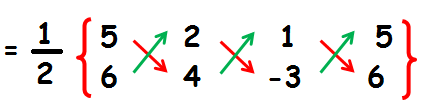
Area of the triangle ABC 

  =  (1/2) {(20 - 6 + 6) - (12 + 4 - 15)}

  =  (1/2) {20 - (16 - 15)}

  =  (1/2) {20 - (1) }

  =  (1/2) {20 - 1}

  =  (1/2)  x 19 

  =  19/2

9.5

So, the area of triangle ABC is 9.5 square units.

Problem 4 : 

Find the area of triangle whose vertices are (1, 3), (-7, 6) and (5, -1).

Solution :

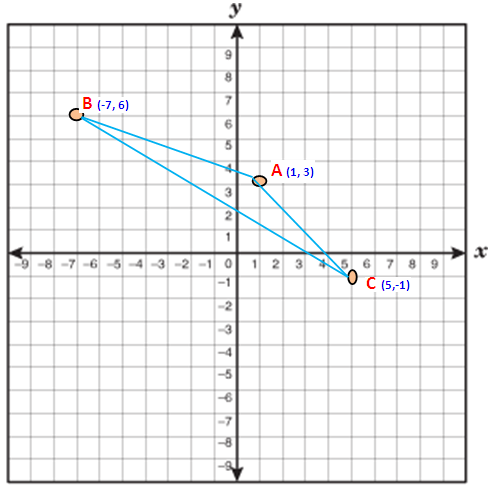
Now we have to take anticlockwise direction. So we have to take the points in the order A (1,3) B (-7,6) and C (5,-1)

x₁ = 1     x₂ = -7      x₃ = 5

y₁ = 3     y₂ = 6       y₃ = -1

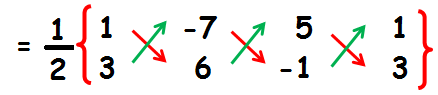
Area of the triangle ACB 

  =  (1/2) {(6 + 7 + 15) - (-21 + 30 - 1)}

  =  (1/2) {28 - ( -22 + 30)}

  =  (1/2) {28 - (8) }

  =  (1/2) {28 - 8}

  =  (1/2)  x 20 

  =  10 Square units.

So, the area of triangle ABC is 10 square units.

Problem 5 :

Find the area of triangle whose vertices are (1, 1), (3, 4) and (5, -2).

Solution :

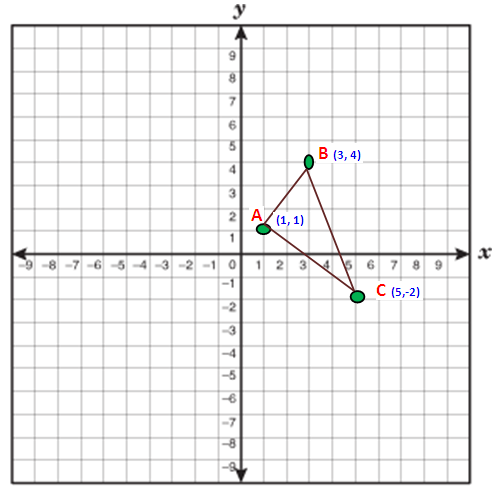
Now we have to take anticlockwise direction. So we have to take the points in the order B (3,3) A (1, 1) and C (5,-2)

x₁ = 3     x₂ = 1      x₃ = 5

y₁ = 3     y₂ = 1       y₃ = -2

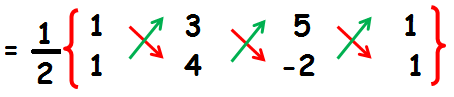
Area of the triangle BAC 

  =  (1/2) {(4 - 6 + 5) - (3 + 20 - 2)}

  =  (1/2) {(9 - 6) - (23 - 2)}

  =  (1/2) {3 - 21}

  =  (1/2) {-18}

  =  -18/2 

  =  9 Square units.

So, the area of triangle ABC is 9 square units.

Problem 6 :

Find the area of triangle whose vertices are (-3, -9), (-1, 6) and (3, 9).

Solution :

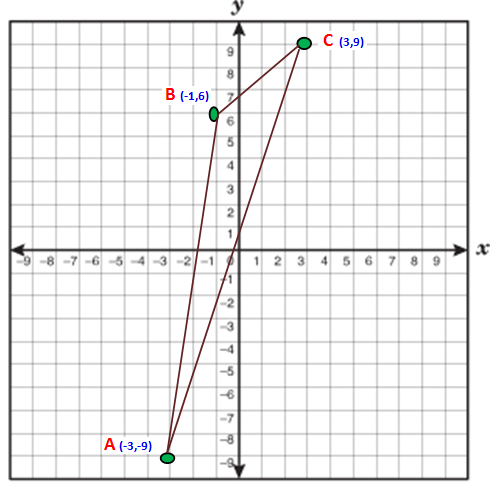
Now we have to take anticlockwise direction. So we have to take the points in the order C (3,9) B (-1,6) and A (-3,-9)

x₁ = 3     x₂ = -1      x₃ = -3

y₁ = 9     y₂ = 6      y₃ = -9

Area of the triangle CBA 

  =  (1/2) {(18 + 9 - 18) - (-9 - 18 - 27)}

  =  (1/2) {9 - ( -54)}

  =  (1/2) {9 + 54}

  =  (1/2) (63)

  =  (63/2) 

  =  31.5 Square units.

So, the area of triangle CBA is 31.5 square units.

Problem 7 :

Find the area of triangle whose vertices are (-3, -9), (3, 9) and (5, -8).

Solution :

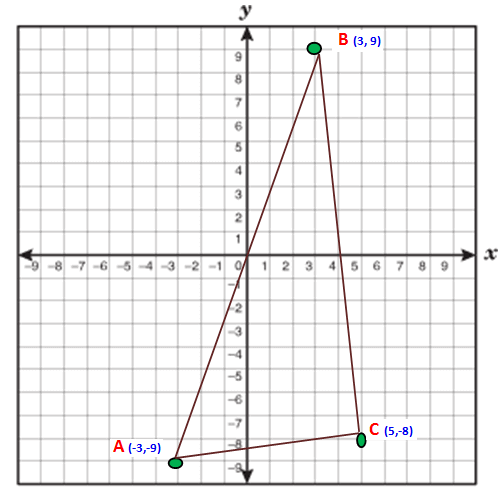
Now we have to take anticlockwise direction. So we have to take the points in the order B (3,9) A (-3,-9) and C (5,-8)

x₁ = 3     x₂ = -3      x₃ = 5

y₁ = 9     y₂ = -9      y₃ = -8

Area of the triangle BAC 

  =  (1/2) {(-27 - 24 + 45) - (-27 - 45 - 24)}

  =  (1/2) {(-51 + 45) - (-96)}

  =  (1/2) {-6 + 96}

  =  (1/2) (90)

  =  (90/2)

  =  45 Square units.

So, the area of triangle BAC is 45 square units.

Problem 8 :

Find the area of triangle whose vertices are (4, 5), (4, 2) and (-2, 2).

Solution :

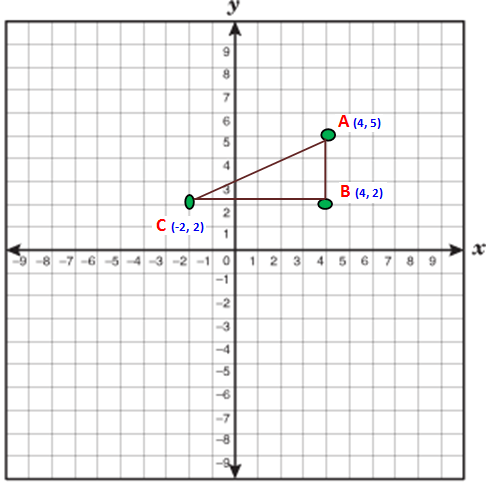
Now we have to take anticlockwise direction. So we have to take the points in the order A (4,5) C (-2,2) and B (4,2)

x₁ = 4     x₂ = -2      x₃ = 4

y₁ = 5     y₂ = 2       y₃ = 2

Area of the triangle ACB 

  =  (1/2) {(8 - 4 + 20) - (-10 + 8 + 8)}

  =  (1/2) {(28 - 4) - ( -10 + 16)}

  =  (1/2) (24 - 6)

  =  (1/2) x 18

  =  (18/2) 

  =  9 Square units.

So, the area of triangle ACB is 9 square units.

Problem 9 :

Find the area of triangle whose vertices are (3, 1), (2, 2) and (2, 0).

Solution :

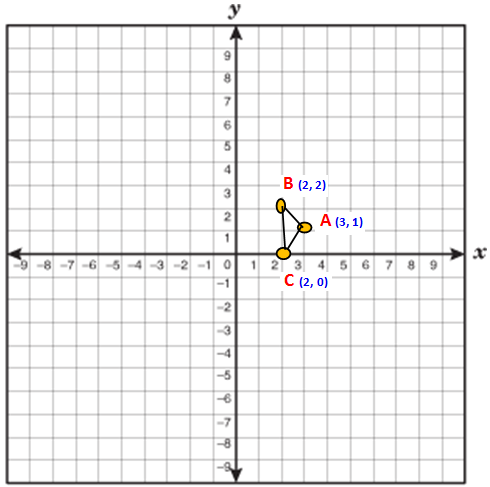
Now we have to take anticlockwise direction. So we have to take the points in the order B (2,2) C (2,0) and A (3,1)

x₁ = 2     x₂ = 2       x₃ = 3

y₁ = 2     y₂ = 0       y₃ = 1

Area of the triangle BCA 

  =  (1/2) {(0 + 2 + 6) - (4 + 0 + 2)}

  =  (1/2) {8 - 6}

  =  (1/2) (2)

  =  (2/2)

  =  1 Square units.

So, the area of triangle ACB is 1 square units.

Problem 10 :

Find the area of triangle whose vertices are (3, 1) (0, 4) and (-3, 1).

Solution :

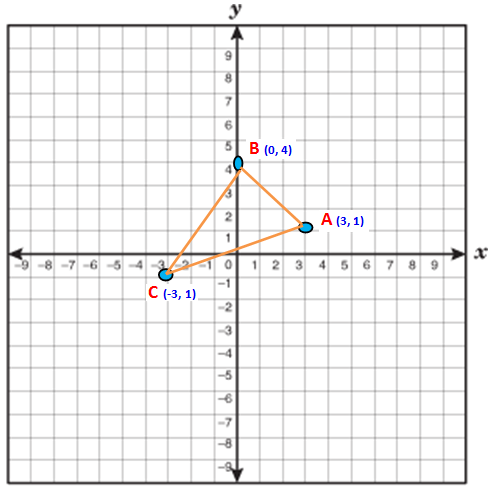
Now we have to take anticlockwise direction. So we have to take the points in the order B (0,4) C (-3,1) and A (3,1)

x₁ = 0     x₂ = -3      x₃ = 3

y₁ = 4     y₂ = 1       y₃ = 1

Area of the triangle BCA 

  =  (1/2) {(0 -3 + 12) - (-12 + 3 + 0)}

  =  (1/2) {9 - ( -12 + 3)}

  =  (1/2) {9 - (-9) }

  =  (1/2) {9 + 9)}

  =  (1/2)  x 18 

  =  9 Square units.

So, the area of triangle BCA is 9 square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.