AREA OF TRIANGLE USING SIN FORMULA PRACTICE QUESTIONS

Problem 1 :

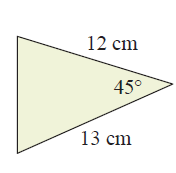
Solution :

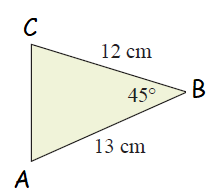
<B  =  45, a  =  12 cm and c  =  13 cm.

Area of triangle  =  (1/2) ⋅ (ac sin B)

=  (1/2) ⋅ (13) ⋅ (12) sin 45

=  (1/2) ⋅ (13) ⋅ (12) (0.707)

=  55.146 cm²

Problem 2 :

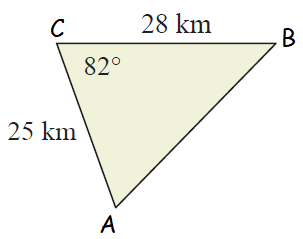
Solution :

<C  =  82, a  =  28 km and c  =  25 km

Area of triangle  =  (1/2) ⋅ (ac sin C)

=  (1/2) ⋅ (28) ⋅ (25) sin 82

=  (1/2) ⋅ (28) ⋅ (25) (0.990)

=  346.5 km²

So, the area of the given triangle is 347 km².

Problem 3 :

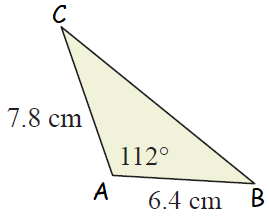
Solution :

<A  =  112, c  =  6.4 cm and b  =  7.8 cm

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (7.8) ⋅ (6.4) sin 112

=  (1/2) ⋅ (7.8) ⋅ (6.4) (0.927)

=  23.13 cm²

So, the area of the given triangle is 23.13 cm².

Problem 4 :

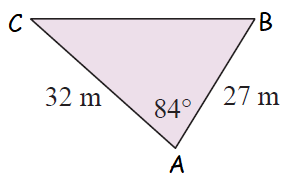
Solution :

<A  =  84, b  =  32 m and c  =  27 m

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (32) ⋅ (27) sin 84

=  (1/2) ⋅ (32) ⋅ (27) (0.994)

=  429.40 m²

So, the area of the given triangle is 430 cm².

Problem 5 :

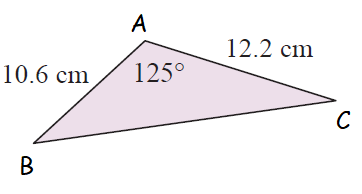
Solution :

<A  =  125, b  =  12.2 cm and c  =  10.6 cm

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (12.2) ⋅ (10.6) sin 125

=  (1/2) ⋅ (12.2) ⋅ (10.6) (0.819)

=  52.95 cm²

So, the area of the given triangle is 53cm².

Problem 6 :

Find the area of a parallelogram with sides 6.4 cm and 8.7 cm and one interior angle 64^o.

Solution :

In a parallelogram, opposite angles are equal and opposite sides are equal.

So, by drawing the diagonal we can divide the parallelogram into two triangles of equal area.

<A  =  64, b  =  6.4 cm and c  =  8.7 cm

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (6.4) (8.7) sin 64

=   (1/2) ⋅ (6.4) (8.7) (0.898)

=  25

Area of parallelogram  =  2(25)

=  50 cm²

Problem 7 :

If triangle ABC has area 150 cm², find the value of x.

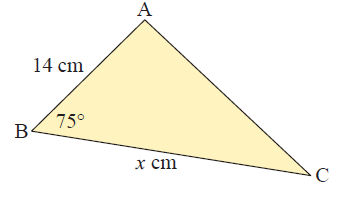
Solution :

<B  =  75, a  =  x cm and c  =  14 cm

Area of triangle  =  (1/2) ⋅ (ac sin B)

=  (1/2) ⋅ (x) (14) sin 75

=   7x (0.965)

=  6.755x

6.755x  =  150

x  =  150/6.755

x  =  22.2 cm

So, the value of x is 22.2 cm.

Problem 8 :

ADB is an arc of the circle with centre C and radius 7.3 cm. AEB is an arc of the circle with centre F and radius 8.7 cm. Find the shaded area

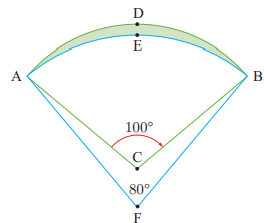
Solution :

<AFB  =  80, BF = AF = 8.7 cm

<ACB  =  100, BF = AF = 7.3 cm

Area of AEBF :

Area of sector = (θ/360) x πr²

= (80/360) x π(8.7)²

= 0.22 x 3.14 x (8.7)²

= 52.28 cm² ----(1)

Joining the points C and F, we get the triangle ACF.

Reflective angle of ACB = 360 - 100

= 260

= 260/2

<ACF = 130

In triangle ACF,

<ACF + <CFA + <FAC = 180

130 + 40 + <FAC = 180

<FAC = 180 - 170

<FAC = 10

Finding area of triangle FAC :

= (1/2) x product of adjacent sides x sin θ

= (1/2) x 8.7 x 7.3 x sin 10

= (1/2) x 8.7 x 7.3 x 0.17

= 5.39

Area of ACBF = 2(5.39)

= 10.78

Area of ADBC = 52.28 - 10.78

 = 41.5 cm²

Area of shaded region = area of small sector

= (100/360) x π(7.3)²

= (5/18) x 3.14 x 53.29 

= 46.48 cm²

Area of shaded region = 46.48 - 41.5

= 4.98 cm²

Problem 9 :

The area of triangle ABC is 86.7 cm². Work out the length of BC. Give your answer correct to 3 significant figures.

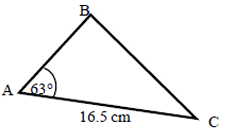
Solution :

= (1/2) x AB x AC x sin θ

86.7 = (1/2) x 16.5 x AB x sin 63

86.7 = 8.25 x AB x 0.89

AB = 86.7 / (8.25 x 0.89)

= 86.7/7.34

= 11.77 cm

Problem 10 :

ABCD is a quadrilateral. AB = 8cm, AD = 15cm and CD = 12cm. Angle ADC = 78° and angle BAC = 20°

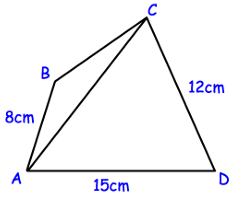
Solution :

Using cosine rule,

AC² = AD² + DC² - 2 (AD)(DC) cos 78

= 15² + 12² - 2 (15)(12) cos 78

= 225 + 144 - 360 (0.20)

= 369 - 72

AC² = 297

AC = √297

AC = 17.23 cm

Area of triangle ADC = (1/2) x AD x CD x sin 78

= (1/2) x 17.23 x 12 x 0.978

= 101.10 cm²

Area of triangle ABC = (1/2) x AC x AB x sin 20

= (1/2) x 17.23 x 8 x 0.34

= 23.43 cm²

area of quadrilateral = 101.10 + 23.43

= 124.53 cm²

Problem 11 :

XY is 8cm, XZ is 10cm, angle YXZ = 79°

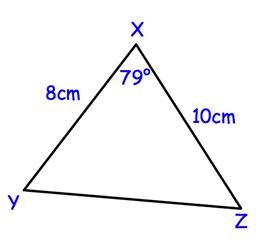
(a) Calculate the area of the triangle XYZ.  .........................cm²

 (b) Calculate the length of YZ.

Solution :

Area of triangle XYZ = (1/2) x XY x XZ x sin 79

= (1/2) x 8 x 10 x 0.98

= 40 x 0.98

= 39.2 cm²

Using cosine rule,

YZ² = XY² + XZ² - 2 (XY)(XZ) cos 79

= 8² + 10² - 2 (8)(10) (0.19)

= 64 + 100 - 160(0.19)

= 164 - 30.4

= 133.6

YZ = √133.6

YZ = 11.55 cm

So, the missing length is 11.55 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.