AREAS OF CIRCLES AND SECTORS WORKSHEET
Problem 1 :
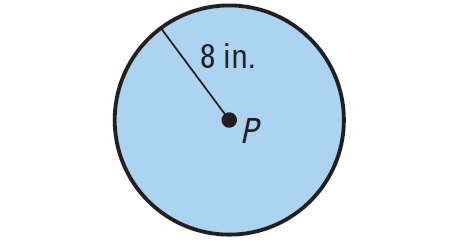
Find the area of the circle shown below.
Problem 2 :
If the area of a circle is 96 square centimeters, find its diameter.
Problem 3 :
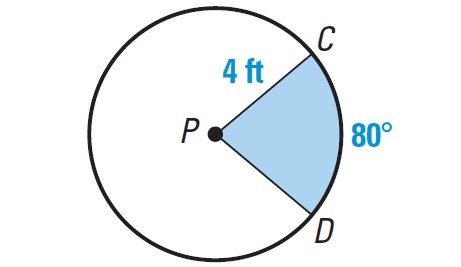
Find the area of the sector shown at the right.
Problem 4 :
A and B are two points on a ⊙P with radius 9 inches and ∠APB = 60°. Find the areas of the sectors formed by ∠APB.
Problem 5 :
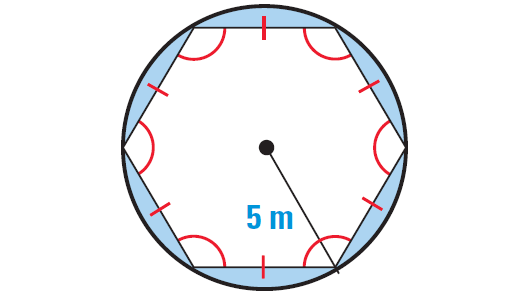
Find the area of the shaded region shown below.
Problem 6 :
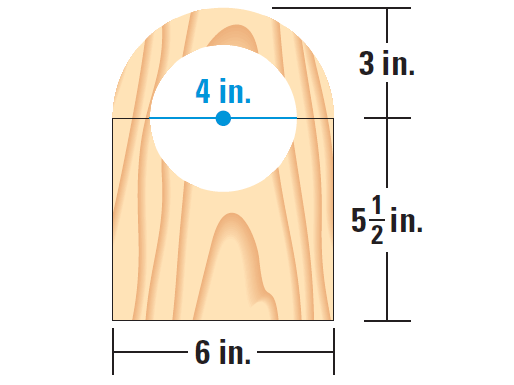
You are cutting the front face of a clock out of wood, as shown in the diagram. What is the area of the front of the case ?

Answers
1. Answer :

Formula area of a circle is given by
A = πr2
Substitute r = 8.
A = π(8)2
A = 64π
Use calculator.
A ≈ 201.06
So, the area is 64π, or about 201.06, square inches.
2. Answer :
Formula area of a circle is given by
A = πr2
Substitute A = 96.
96 = πr2
Divide each side π.
96/π = πr2/π
96/π = r2
Use calculator.
30.56 ≈ r2
Take square root on each side.
5.53 ≈ r
So, the diameter of the circle is about 2(5.53), or about 11.06, centimeters.
3. Answer :

Sector CPD intercepts an arc whose measure is 80°. The radius is 4 feet.
Formula for area of a sector is given by
A = [m∠arc CD/360°] ⋅ πr2
Substitute m∠arc CD = 80° and r = 4.
A = [80°/360°] ⋅ π(4)2
A = (2/9) ⋅ 16π
Use calculator.
A ≈ 11.17
So, the area of the sector is about 11.17 square feet.
4. Answer :
Draw a diagram of ⊙P and ∠APB. Shade the sectors. Label a point Q on the major arc.
Find the measures of the minor and major arcs.
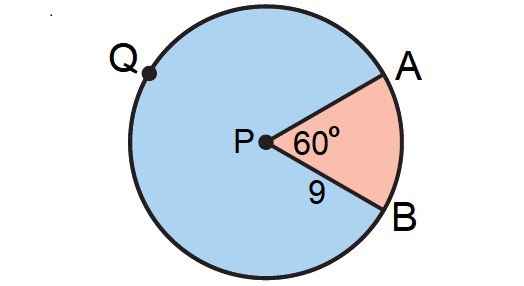
Because m∠APB = 60°, we have
m∠arc AB = 60°
and
m∠AQB = 360° - 60° = 300°
Use the formula for the area of a sector.
A = [m∠arc CD/360°] ⋅ πr2
Substitute m∠arc CD = 80° and r = 4.
A = [80°/360°] ⋅ π(4)2
A = (2/9) ⋅ 16π
Use calculator.
A ≈ 11.17
So, the area of the sector is about 11.17 square feet.
|
Area of Smaller Sector A = 60°/360° ⋅ π(9)2 A = 1/6 ⋅ π ⋅ 81 A ≈ 42.41 square inches |
Area of Larger Sector A = 300°/360° ⋅ π(9)2 A = 5/6 ⋅ π ⋅ 81 A ≈ 212.06 square inches |
5. Answer :

The diagram shows a regular hexagon inscribed in a circle with radius 5 meters. The shaded region is the part of the circle that is outside of the hexagon.
Area of shaded region = Area of circle - Area of hexagon
Area of shaded region = πr2 - 1/2 ⋅ a ⋅ p
Radius of the circle is 5 and the apothem of a hexagon is
= 1/2 ⋅ side length ⋅ √3
= 1/2 ⋅ 5 ⋅ √3
= 5√3/2
So, the area of the shaded region is
= [π ⋅ 52] - [1/2 ⋅ (5√3/2) ⋅ (6 ⋅ 5)]
= 25π - 75√3/2
Use calculator.
≈ 13.59
So, the area of the shaded region is about 13.59 square meters.
6. Answer :

The front of the case is formed by a rectangle and a sector, with a circle removed. Note that the intercepted arc of the sector is a semicircle.
So, the required area is
= Area of rectangle + Area of sector - Area of circle
= [6 ⋅ 11/2] + [180°/360° ⋅ π ⋅ 32] - [π ⋅ (1/2 ⋅ 4)2]
= 33 + 9/2 ⋅ π - 4π
Use calculator.
≈ 34.57
The area of the front of the case is about 34.57 square inches.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 8)
Jan 30, 25 09:48 AM
AP Calculus AB Problems with Solutions (Part - 8) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 29, 25 06:00 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 105)
Jan 29, 25 05:52 AM
Digital SAT Math Problems and Solutions (Part - 105)
