ARGUMENT OF A COMPLEX NUMBER IN DIFFERENT QUADRANTS
Let (r, θ) be the polar co-ordinates of the point.
P = P(x, y) in the complex plane corresponding to the complex number
z = x + iy
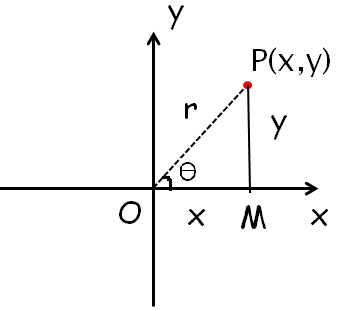
cos θ = Adjacent side/hypotenuse side ==> OM/MP ==> x/r
sin θ = Opposite side/hypotenuse side ==> PM/OP ==> y/r
x = r cos θ and y = r sin θ
tan θ = y/x
θ = tan−1 y/x
is called the amplitude or argument of z = x + iy
denoted by amp z or arg z and is measured as the angle which the line OP makes with the positive x-axis (in the anti clockwise sense).
How to find argument of complex number ?
Usually we have two methods to find the argument of a complex number
(i) Using the formula θ = tan−1 y/x
here x and y are real and imaginary part of the complex number respectively.
This formula is applicable only if x and y are positive.
But the following method is used to find the argument of any complex number.
Argument of a complex number in different quadrants
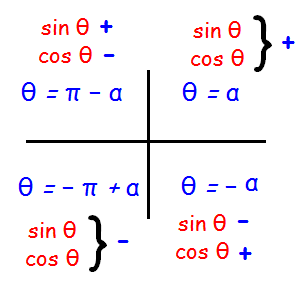

To find the modulus and argument for any complex number we have to equate them to the polar form
r (cos θ + i sin θ)
Here r stands for modulus and θ stands for argument
Let us see some example problems to understand how to find the modulus and argument of a complex number.
Example 1 :
Find the modulus and argument of the complex number
- √2 + i √2
Solution :
- √2 + i √2 = r (cos θ + i sin θ) ----(1)
r = √ [(-√2)² + √2²] = √(2 + 2) = √4 = 2
r = 2
Apply the value of r in the first equation
- √2 + i √2 = 2 (cos θ + i sin θ)
- √2 + i √2 = 2 cos θ + i 2 sin θ
Equating the real and imaginary parts separately
|
2 cos θ = - √2 cos θ = - √2/2 cos θ = - 1/√2 |
2 sin θ = √2 sin θ = √2/2 sin θ = 1/√2 |
Since sin θ is positive and cos θ is negative the required and θ lies in the second quadrant.
θ = Π - α
Here α is nothing but the angles of sin and cos for which we get the value 1/√2
θ = Π - (Π/4)
θ = (4Π-Π)/4 ==> 3Π/4
Modulus = 2 and argument = 3Π/4
Hence - √2 + i √2 = 2 (cos 3Π/4 + i sin 3Π/4)
Example 2 :
Find the modulus and argument of a complex number
1 + i √3
Solution :
1 + i √3 = r (cos θ + i sin θ) ----(1)
r = √ [(1)² + √3²] = √(1 + 3) = √4 = 2
r = 2
Apply the value of r in the first equation
1 + i √3 = 2 (cos θ + i sin θ)
1 + i √3 = 2 cos θ + i 2 sin θ
Equating the real and imaginary parts separately
|
2 cos θ = 1 cos θ = 1/2 |
2 sin θ = √3 sin θ = √3/2 |
Since sin θ and cos θ are positive, the required and θ lies in the first quadrant.
θ = α
Here α is nothing but the angles of sin and cos for which we get the values 1/2 and √3/2 respectively.
θ = Π/3
Modulus = 2 and argument = Π/3
Hence - √2 + i √2 = 2 (cos Π/3 + i sin Π/3)
Example 3 :
Find the modulus and argument of the complex number
-1 - i √3
Solution :
-1 - i √3 = r (cos θ + i sin θ) ----(1)
r = √ [(-1)² + (-√3)²] = √(1 + 3) = √4 = 2
r = 2
Apply the value of r in the first equation
-1 - i √3 = 2 (cos θ + i sin θ)
-1 - i √3 = 2 cos θ + i 2 sin θ
Equating the real and imaginary parts separately
|
2 cos θ = -1 cos θ = -1/2 |
2 sin θ = -√3 sin θ = -√3/2 |
Since sin θ and cos θ are negative the required and θ lies in the third quadrant.
θ = -Π + α
Here α is nothing but the angles of sin and cos for which we get the values √3/2 and 1/2 respectively.
θ = - Π + α
= - Π + Π/3 ==> (-3Π+Π)/3 ==> -2Π/3
Modulus = 2 and argument = -2Π/3
Hence - 1 - i √3 = 2 (cos (-2Π/3) + i sin (-2Π/3))
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
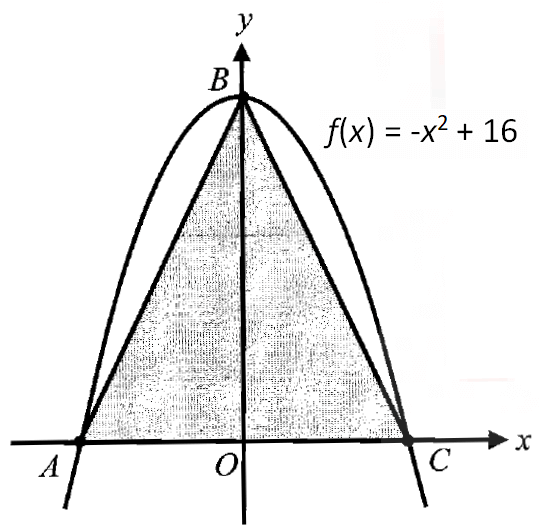
Digital SAT Math Problems and Solutions (Part - 143)
Apr 13, 25 12:01 PM
Digital SAT Math Problems and Solutions (Part - 143) -
Quadratic Equation Problems with Solutions
Apr 12, 25 08:21 PM
Quadratic Equation Problems with Solutions -
Digital SAT Math Problems and Solutions (Part - 142)
Apr 11, 25 06:26 PM
Digital SAT Math Problems and Solutions (Part - 142)