ARITHMETIC MEAN WORKSHEET

1. Compute arithmetic mean for the following data.

58, 62, 48, 53, 70, 52, 60, 84, 75

2. Compute the mean weight of a group of students of an university from the following data. 

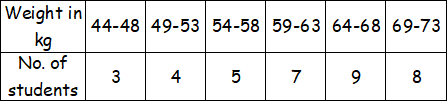
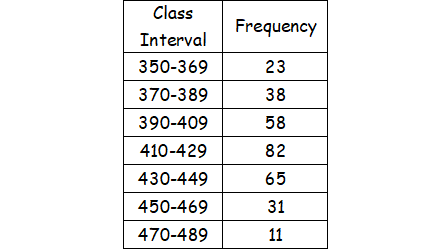
3. Find the arithmetic mean for the following distribution.

4. Two variables x and y are related by 2x + 3y + 7 = 0. If the arithmetic mean of x is 15, then find the arithmetic mean of y. 

5. The mean salary for a group of 40 female workers is $5200 per month and that for a group of 60 male workers is $6800 per month. What is the combined mean salary?

6. The average salary of 50 men was $80 but it was found that salary of 2 of them were $46 and $28 which was wrongly taken as $64 and $82. The revised salary is

a)  80    b)  78.56     c)  85.26    d)  82.92

7. The mean weight of 15 students is 110 kg. The mean weight of 5 of them is 100 kg and of another five students is 125 kg, then the mean weight of remaining student is 

a) 120     b)  105    c)  115    d) none

8. The mean of first three term is 14 and mean of next two terms is 18. The mean of all five term is 

a)  14.5    b)  15     c)  14    d) 15.6

9. The mean salary of a group of 50 persons is $5850. Later on it is discovered that the salary of one employee has been wrongly taken as $8000 instead of $7800. The corrected mean salary is :

a)  $5854    b)  $5846    c)  $5650    d) None

10. The mean of the following data is 6. Find the value of P

x : 2     4     6    10   P + 5

f :  3     2    3       1      2

1. Answer : 

Formula to find geometric mean : 

x̄ = ∑x/n

Fitting the given data in to the above formula, we get

x̄ = (58 + 62 + 48 + 53 + 70 + 52 + 60 + 84 + 75)/9

= 562/9

≈ 62.44

2. Answer : 

Computation of mean weight of 36 students.

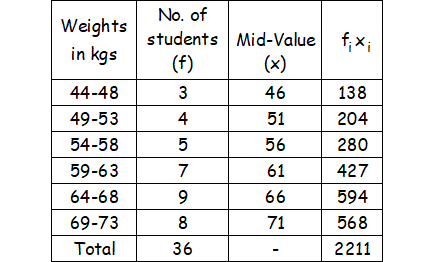
For to find arithmetic mean for the above data :

x̄ = ∑fx/N

N = ∑f = 36

∑fx = 2211

Mean weight :

x̄ = 2211/36

≈ 61.42 kg

3. Answer :

Computation of arithmetic mean :

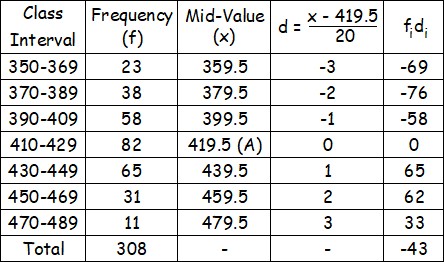
Formula to find arithmetic mean for the above data : 

x̄ = A + (∑fd/N) ⋅ C

A  =  Average of the largest and smallest mid-values

A = (479.5 + 359.5)/2 = 419.5

N = ∑f = 308

∑fd = - 43

C = 20

Arithmetic mean :

x̄ = 419.50 +(-43/308) ⋅ 20

= 419.50 - 860/308

≈ 416.71

4. Answer :

In 2x + 3y + 7 = 0, x and y are in linear relationship.

If two variables are in linear relationship, their arithmetic means also will be in the same linear relationship.  

2x + 3y + 7 = 0

Solve for y. 

3y = -2x - 7

y = (-2x - 7)/3

Arithmetic mean of y = (-7 - 2x̄)/3

Substitute x̄ = 15.

= (-7 - 2x15)/3

= (-7 - 30)/3

= -37/3

5. Answer :

Formula to find combined arithmetic mean :

x̄ = (n₁x̄₁ + n₂x̄₂)/(n₁ + n₂)

As given

n₁ = 40, n₂ = 60, x̄₁ = 5200 and x̄₂ = 6800

Combined mean salary : 

x̄ = (40 ⋅ 5200 + 60 ⋅ 6800)/(40 + 60)

= (208000 + 408000)/100

= 616000/100

= $6160

6. Answer :

Mean = ∑x/N

80 = ∑x / 50

80(50) = ∑x

∑x = 4000

Corrected ∑x = 4000 - (64 + 82) + (46 + 28)

= 4000 - 146 + 74

= 3854 + 74

= 3928

new mean = 3928/50

= 78.56

So, the revised salary is $78.56

7. Answer :

Total weight of 1st five students = 5 x 100

= 500

Total weight of another five students = 5 x 125

= 625

Total weight of 10 students = 500 + 625

= 1125

Total weight of 15 students = 15 x 110

= 1650

Total weight of remaining 5 students = 1650 - 1125

= 525

Mean weight of remaining 5 students = 525/5

= 105

So, the mean weight of remaining 5 students is 105

8.Answer :

Mean of first three items = 14

Mean = ∑x/n

14 = ∑x/3

14 (3) = ∑x

∑x = 42

Sum of three items = 42

Mean of next two items = 18

18 = ∑x/2

18(2) = ∑x

∑x = 36

Sum of next two terms = 36

Sum of all 5 terms = 42 + 36

= 78

Mean of 5 terms = 78/5

= 15.6

So, option d is correct.

9.Answer :

Mean of 50 persons = 5850

Sum of salary of 50 persons = ∑x/50

5850 = ∑x/50

∑x = 5850(50)

= 292500

Correct sum = 292500 - incorrect value + correct value

= 292500 - 8000 + 7800

= 292300

Correct mean = 292300/50

= 5846

x : 2     4     6    10   P + 5

f :  3     2    3       1      2

Mean = ∑fx/∑f

= (6 + 8 + 18 + 10 + 2P + 10)/11

6 = (2P + 52)/11

6(11) = 2P  +52

2P + 52 = 66

2P = 66 - 52

2P = 14

P = 7

So, the value of P is 7.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.