ARITHMETIC MEAN

Arithmetic mean (AM) is one of the measures of central tendency which can be defined as the sum of all observations divided by the number of observations. 

Let the  variable x assume n values  as given below.

x₁, x₂, x₃, ............x_n

Then, the AM of 'x' to be denoted by x̄ and it is given by

x̄ = (x₁ + x₂ + x₃ + ............ + x_n)/n

= ∑x_i/n

In case of a simple frequency distribution relating to an attribute, we have 

x̄ = (f₁x₁ + f₂x₂ + f₃x₃ + ............ + f_nx_n)/N

= ∑f_ix_i/N

where N = f₁ + f₂ + f₃ + ............ + f_n.

In the above frequency distribution, if the original value 'x' is changed to 'd', due to the shift of origin (assumed mean) by A units  and  scale (class length ) by C units, then the formula for AM is given by

x̄ = A + ∑f_id_i/N + C

where

d_i = (x_i - A)/C

A = assumed mean

C = class length

Properties of Arithmetic Mean

Property 1 :

If all the observations assumed by a variable are constants, say 'k', then arithmetic mean is also 'k'. 

For example, if the height of every student in a group of 10 students is 170 cm, the mean height is, of course 170 cm. 

Property 2 :

The algebraic sum of deviations of a set of observations from their arithmetic mean is zero. 

That is, for unclassified data, ∑(x - x̄) = 0.

And for a grouped frequency distribution, ∑f(x - x̄) = 0.

For example,  if a variable 'x' assumes five observations, say 10, 20, 30, 40, 50, then x̄ = 30.

The deviations of the observations from arithmetic mean (x - x̄) are -20, -10, 0, 10, 20. 

Now, ∑(x - x̄) = (-20) + (-10) + 0 + 10 + 20 = 0.

Property 3 :

Arithmetic mean is affected due to a change of origin and/or scale which implies that if the original variable 'x' is changed to another variable 'y' effecting a change of origin, say 'a' and scale, say 'b', of 'x'. That is  y = a + bx.

Then we have,

Arithmetic mean of 'y' = a + bx̄

For example, if it is known that two variables x and y are related by 2x + 3y + 7 = 0 and x̄ = 15, then

Arithmetic mean of 'y' = (-7 - 2x̄)/3

Substitute x̄ = 15.

= (-7 - 2x15)/3

= (-7 - 30)/3

= -37/3

Property 4 : 

If there are two groups containing n₁ and n₂ observations with x̄₁ and x̄₂ as the respective arithmetic means, then the combined arithmetic mean is given by

x̄ = (n₁x̄₁ + n₂x̄₂)/(n₁ + n₂)

This property could be extended to more than two groups and we may write it as 

x̄ = ∑nx̄/∑n

where 

∑nx̄ = n₁x̄₁ + n₂x̄₂ + ........

∑n = n₁ + n₂ + ........

Note : 

The best measure of central tendency, usually, is the AM. It is rigidly defined, based on all the observations, easy to comprehend, simple to calculate and amenable to mathematical properties.

However, AM has one drawback in the sense that it is very much affected by sampling fluctuations. In case of frequency distribution, mean cannot be advocated for open-end classification.

For open end classification, the most appropriate measure of central tendency is median. 

Practice Problems

Problem 1 : 

Compute arithmetic mean for the following data.

58, 62, 48, 53, 70, 52, 60, 84, 75

Solution : 

Formula to find geometric mean : 

x̄ = ∑x/n

Fitting the given data in to the above formula, we get

x̄ = (58 + 62 + 48 + 53 + 70 + 52 + 60 + 84 + 75)/9

= 562/9

≈ 62.44

Problem 2 : 

Compute the mean weight of a group of students of an university from the following data. 

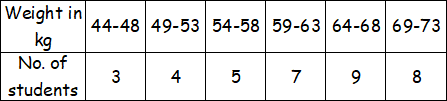
Solution : 

Computation of mean weight of 36 students.

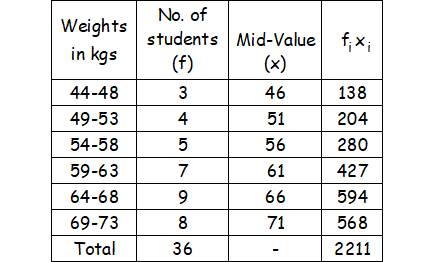
For to find arithmetic mean for the above data :

x̄ = ∑fx/N

N = ∑f = 36

∑fx = 2211

Mean weight :

x̄ = 2211/36

≈ 61.42 kg

Problem 3 : 

Find the arithmetic mean for the following distribution.

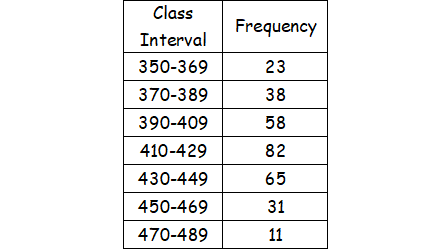
Solution :

Computation of arithmetic mean :

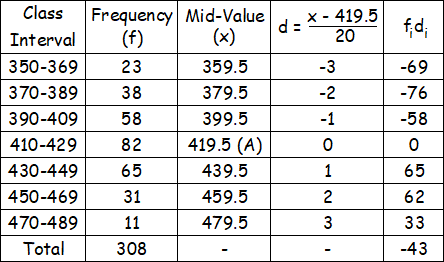
Formula to find arithmetic mean for the above data : 

x̄ = A + (∑fd/N) ⋅ C

A  =  Average of the largest and smallest mid-values

A = (479.5 + 359.5)/2 = 419.5

N = ∑f = 308

∑fd = - 43

C = 20

Arithmetic mean :

x̄ = 419.50 +(-43/308) ⋅ 20

= 419.50 - 860/308

≈ 416.71

Problem 4 :

The average of 10 observations is 14.4. IF the average of first 4 observations is 16.5. The average of remaining 6 observations is 

a)  13.6     b)  13    c)  13.2    d) 12.5

Solution :

Given that n1 = 4, n2 = 6

Average of first 10 observations = 14.4

Let x be the average of next set of observations.

Combined average = [4(16.5) + 6x]/(4 + 6)

14.4 = (66 + 6x)/10

14.4(10) = 66 + 6x

144 - 66 = 6x

78 = 6x

x = 78/6

x = 13

Problem 5 :

Mean for the data 6, 4, 1, 6, 5, 10, 6 is 5. When each observation added by, what is the mean of the data.

a)  5   b)  6    c)  7    d)  10

Solution :

Original mean = 5

After adding some same constants with each elements, the new mean will also be added by the same constant.

New mean = 5 + 2

= 7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.