ARITHMETIC SEQUENCES AND SERIES WORKSHEET

1.  Is the sequence arithmetic ? If so, what is the common difference ? What is the next term in the sequence ?

3, 8, 13, 18, 23,.............

2.  An arithmetic sequence has first term 7 and common difference 8. Find the 10^th term.

3.  The third term of an arithmetic sequence is 10 and the 15^th term is 46. Write the sequence. 

4. Find the number of terms in the arithmetic sequence : 

1, 4, 7,............ , 100

5.  An arithmetic sequence has first term 5 and common difference –2. Find the sum of the first 10 terms.

6. An arithmetic sequence has first term 10 and last term 1000. If there are 30 terms, find the sum of all the terms.

7.  The sum of the first n terms of the sequence 3, 7, 11, 15… is 465. Find n.

8. Find the sum of the terms in the arithmetic sequence :

4, 10, 16, 22, ..................., 286

9.  Find the sum of the terms in the arithmetic sequence :

5, 9, 13, 17, 21

What is the general formula for an arithmetic series ?

10. If the sum of first n terms of an arithmetic sequence is 3n² + 5n, find the first term and common difference. 

Detailed Answer Key

1. Answer :

This is a sequence, a function whose domain is the Natural numbers. 

Create a table that shows the term number, or domain, and the term, or range.   

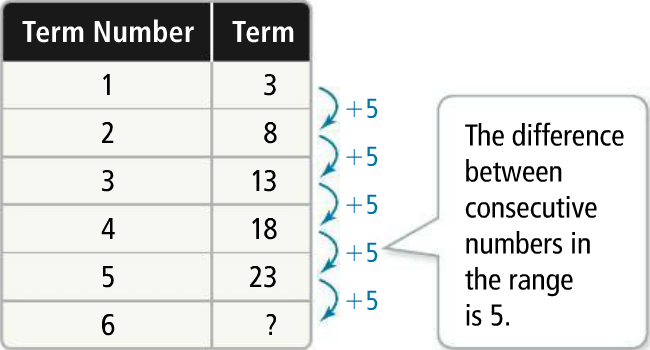
An arithmetic sequence is a sequence with a constant difference between consecutive terms. The difference is known as the common difference, or d.  

This sequence is an arithmetic sequence with common difference,

d = 5 

The next term in the sequence is

23 + 5, or 28

2. Answer : 

Formula for the n^th term of an arithmetic sequence :

a_n = a₁ + (n - 1)d

Substitute n = 10, a₁ = 7 and d = 8.

a₁₀ = 7 + (10 - 1)8

= 7 + (9)8

= 7 + 72

= 79

The 10^th term of the given arithmetic sequence is 79.

3. Answer : 

a₃ = 10  and  a₁₅ = 46

Solve (1) and (2). 

(2) - (1) : 

(a₁ + 14d) - (a₁ + 2d) = 46 - 10

a₁ + 14d -a₁ + 2d = 36

12d = 36

d = 3

Substitute d = 3 in (1). 

a₁ + 2(3) = 10

a₁ + 6 = 10

a₁ = 4

Arithmetic sequence : 

a₁, a₁ + d, a₁ + 2d, ..........

Substitute a₁ = 4 and d = 3. 

4, 4 + 3, 4 + 2(3), ..........

4, 7, 4 + 6, ..........

4, 7, 11, ..........

4. Answer : 

1, 4, 7, ............ , 100

This is an arithmetic sequence with a₁ = 1 and d = 3.

Let a_n = 100.

a_n  =  100

a₁ + (n - 1)d  =  100

Substitute a₁ = 1 and d = 3.

1 + (n - 1)3  =  100

1 + 3n - 3  =  100

3n - 2  =  100

3n  =  102

n  =  34

There are 34 terms in the given arithmetic sequence. 

5. Answer : 

An arithmetic sequence has first term 5 and common difference –2. Find the sum of the first 10 terms.

Formula for sum of first n terms of an arithmetic sequence : 

S_n = (n/2)[2a₁ + (n - 1)d]

Substitute n = 10, a₁ = 5 and d = -2.

S₁₀ = (10/2)[2(5) + (10 - 1)(-2)]

= 5[10 + 9(-2)]

= 5[10 - 18]

=  5[-8]

=  -40

6. Answer :

Formula for the sum of the first n terms of an arithmetic sequence.

S_n = (n/2)[a₁ + a_n]

Substitute n = 30, a₁ = 10 and a_n = 1000.

S₃₀ = (30/2)[10 + 1000]

=  15[1010]

=  15150 

7. Answer :

3, 7, 11, 15, ............

This is an arithmetic sequence with a₁ = 3 and d = 4.

S_n  =  465

(n/2)[2a₁ + (n - 1)d]  =  465

Substitute a₁ = 3 and d = 4.

(n/2)[2(3) + (n - 1)(4)] = 465

(n/2)[6 + 4n - 4] = 465

(n/2)[4n + 2] = 465

n[2n + 1] = 465

2n² + n = 465

2n² + n - 465 = 0

Factor and solve. 

2n² + 31n - 30n - 465 = 0

n(2n + 31) - 15(n + 31) = 0

(n + 31)((n - 15) = 0

Because n stands for number of terms, it can not be a negative value. 

So, n = 15.

8. Answer : 

4, 10, 16, 22, .................., 286

In this arithmetic sequence a₁ = 4, a_n = 286 and d  = 6.

a_n = 286

a₁ + (n - 1)d = 286

Substitute a₁ = 4 and d = 6.

4 + (n - 1)6 = 286

4 + 6n - 6 = 286

6n - 2 = 286

6n = 288

n = 48

Formula for the sum of the first n terms of an arithmetic sequence.

S_n = (n/2)[a₁ + a_n]

Substitute n = 48, a₁ = 4 and a_n = 286.

S₄₈ = (48/2)[4 + 286]

= 24[290]

= 6960

9. Answer :

A finite series is the sum of the terms in a finite sequence. A finite arithmetic series is the sum of the terms in an arithmetic sequence. For the sum of n numbers in a sequence, we can use recursive formula or simply add the terms. 

Sn = + a₁ + a₂ + a₃ + a₄ + ...................... + a_n

(This represents a partial sum of a series, because it is the sum of a finite number of terms, n, in the series)

5 + 9 + 13 + 17 + 21 = 65

To find the sum of a series with many terms, we can use an explicit definition. 

To find the explicit definition for the sum, use the Commutative Property of Addition and reverse the order of the terms in the recursive series. 

S₅ = 21 + 17 + 13 + 9 + 5

Add the two expressions for the series, so we are adding the first term to last term and the second term to the second-to-last term, and so on.    

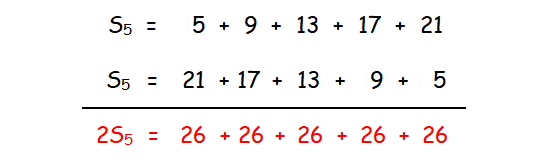
Simplify. 

2 ⋅ S₅ = 5(26)

2 ⋅ S₅ = 5(5 + 21)

Divide each side by 2. 

S₅ = 5(5 + 21)/2

Write the general formula. 

S_n = (n/2)(a₁ + a_n)

10. Answer : 

S_n = 3n² + 5n

Substitute n = 1.

S₁ = 3(1)² + 5(1)

= 3(1) + 5

= 3 + 5

= 8

So, the first term is 8. That is, a₁ = 8.

Substitute n = 2.

S₂ = 3(2)² + 5(2)

= 3(4) + 10

= 12 + 10

= 22

Sum of first two terms is 22.

a₁ + a₂ = 22

Substitute a₁ = 8. 

8 + a₂ = 22

a₂ = 14

Common difference : 

d = a₂ - a₁

= 14 - 8

= 6

The first term and common difference are 8 and 6 respectively.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.