ARITHMETIC SEQUENCES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A sequence is a list of numbers that may form a pattern. Each number in a sequence is a term.
When the terms of a sequence differ by the same nonzero number d, the sequence is an arithmetic sequence and d is the common difference. The distances in the table form an arithmetic sequence with d = 0.2.
The variable a is often used to represent terms in a sequence. The variable a7, read “a sub 7,” is the seventh term in a sequence. To designate any term, or the nth term, in a sequence, you write an, where n can be any number.
To find a term in an arithmetic sequence, add d to the previous term.
Finding a Term of an Arithmetic Sequence
The nth term of an arithmetic sequence with common difference d is
an = an-1 + d
Identifying Arithmetic Sequences
Determine whether each sequence appears to be an arithmetic sequence. If so, find the common difference and the next three terms in the sequence.
Example 1 :
15, 10, 5, 0, ........
Solution :
Step 1 :
15, 10, 5, 0, ........
Find the difference between successive terms.
10 - 15 = -5
5 - 10 = -5
0 - 5 = -5
The common difference is -5.
Step 2 :
Use the common difference to find the next 3 terms.
Add -5 to each term to find the next term.
an = an-1 + d
0 + (-5) = 0 - 5 = -5
-5 + (-5) = -5 - 5 = -10
-10 + (-5) = -10 - 5 = -15
The sequence appears to be an arithmetic sequence with a common difference of -5.
The next 3 terms are -5, -10, -15.
Example 2 :
2, 5, 10, 17, ........
Solution :
2, 5, 10, 17, ........
Find the difference between successive terms.
5 - 2 = 3
10 - 5 = 5
17 - 10 = 7
The difference between successive terms is not the same.
This sequence is not an arithmetic sequence.
To find the nth term of an arithmetic sequence when n is a large number, you need an equation or rule. Look for a pattern to find a rule for the sequence below.
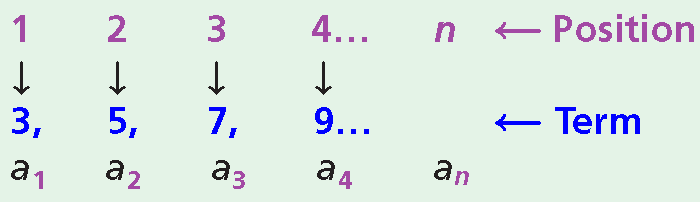
The sequence starts with 3. The common difference d is 2. You can use the first term and the common difference to write a rule for finding an.

The pattern in the table shows that to find the nth term, add the first term to the product of (n - 1) and the common difference.
Finding the nth Term of an Arithmetic Sequence
The nth term of an arithmetic sequence with common difference d and first term a1 is
an = a1 + (n - 1)d
Find the indicated term of each arithmetic sequence.
Example 3 :
25th term : 6, 2, -2, -6,.........
Solution :
Step 1 : Find the common difference.
2 - 6 = -4
-2 - 2 = -4
-6 - (-2) = -4
The common difference is -4.
Step 2 : Find the 25th term.
Write the rule to find the nth term.
an = a1 + (n - 1)d
Substitute 6 for a1, 25 for n, and -4 for d.
a25 = 6 + (25 - 1)(-4)
Simplify the expression in parentheses.
a25 = 6 + (24)(-4)
Multiply.
a25 = 6 - 96
Subtract.
a25 = -90
Example 4 :
16th term : a1 = 8; d = 5
Solution :
Write the rule to find the nth term.
an = a1 + (n - 1)d
Substitute 8 for a1, 16 for n, and 5 for d.
a16 = 8 + (16 - 1)(5)
Simplify the expression in parentheses.
a16 = 8 + (15)(5)
Multiply.
a16 = 8 + 75
Add.
a16 = 83
Travel Application
Example 5 :
The odometer on a car reads 60,180 on day 1. Every day, the car is driven 60 miles. If this pattern continues, what is the odometer reading on day 22?
Solution :
Notice that the sequence for the situation is arithmetic with d = 60 because the odometer reading will increase by 60 miles per day. Since the odometer reading on day 1 is 60,180 miles, a1 = 60,180. Because you want to find the odometer reading on day 22, you will need to find the 20th term of the sequence, so n = 22.
Write the rule to find the nth term.
an = a1 + (n - 1)d
Substitute 60,180 for a1, 22 for n, and 60 for d.
a22 = 60,180 + (22 - 1)(60)
Simplify the expression in parentheses.
a22 = 60,180 + (21)(60)
Multiply.
a22 = 60,180 + 1,260
Add.
a22 = 61,440
The odometer will read 61,440 miles on day 22.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


