ARITHMETIC SERIES WORD PROBLEMS WITH ANSWERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
A man repays a loan of 65,000 by paying 400 in the first month and then increasing the payment by 300 every month. How long will it take for him to clear the loan?
Solution :
For the first month he is paying = 400
payment of second month = 400 + 300 = 700
payment of 3rd month = 700 + 300 = 1000
400 + 700 + 1000, ................
loan amount = 65000
(n/2)[2a + (n - 1)d] = 65000
(n/2)[2(400) + (n - 1)300] = 65000
(n/2)[800 + 300n - 300] = 65000
(n/2)[500 + 300n] = 65000
(n/2)[5 + 3n] = 650
n[5 + 3n] = 1300
5n + 3n2 = 1300
3n2 + 5n - 1300 = 0
3n2 - 60n + 65n - 1300 = 0
3n(n - 20) + 65(n - 20) = 0
(n - 20) (3n + 65) = 0
n = 20 or n = -65/3 (not acceptable)
So, he will clear the loan amount in 20 months.
Question 2 :
A brick staircase has a total of 30 steps. The bottom step requires 100 bricks. Each successive step requires two bricks less than the previous step.
(i) How many bricks are required for the top most step?
(ii) How many bricks are required to build the stair case?
Solution :
Let "l" be the number of bricks in the last step
Number of bricks in the 1st step (a) = 100
Number of bricks in the 2nd step = 100 - 2 = 98
d = 98 - 100 = -2
number of steps (n) = 30
(i)
t30 = a + 29d
= 100 + 29(-2)
= 100 - 58
= 42
So, we will have 42 bricks in the top most step.
(ii) How many bricks are required to build the stair case?
Sn = (n/2)[a + l]
= (30/2)[100 + 42]
= 15(142)
= 2130
Question 3 :
If S1, S2, S3,....Sm are the sums of n terms of m A.P.’s whose first terms are 1,2, 3,...m and whose common differences are 1, 3, 5,..., (2m -1) respectively, then show that S1 + S2 + S3 +............Sm = (mn/2)(1 + mn)
Solution :
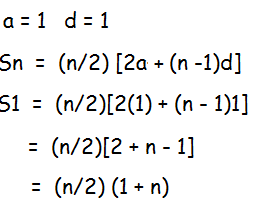
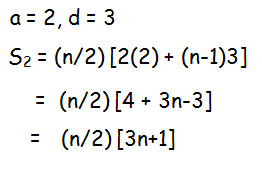
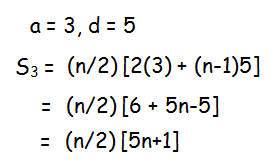
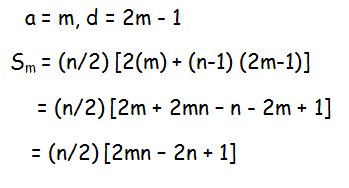
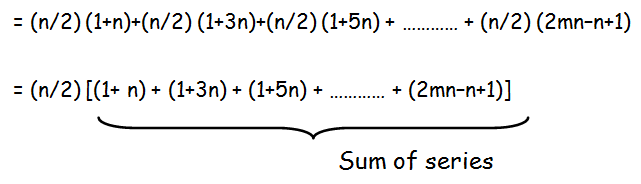
n = [(l-a)/d] + 1
n = [((2mn - n + 1) - (1 + n))/2n] + 1
n = [(2mn - n + 1 - 1 - n)/2n] + 1
n = [(2mn - 2n)/2n] + 1
n = (m - 1) + 1
n = m
S1 + S2 + S3 +............Sm
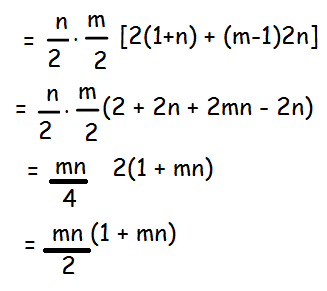
Hence proved.
Question 4 :
Find the sum
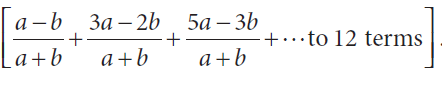
Solution :
a = (a-b)/(a+b)
d = (3a-2b)/(a+b) - (a-b)/(a+b)
d = [3a - 2b -(a - b)]/(a + b)
d = [3a - 2b -a + b]/(a + b)
d = (2a - b) / (a + b)
Sn = (n/2)[2a + (n - 1)d]
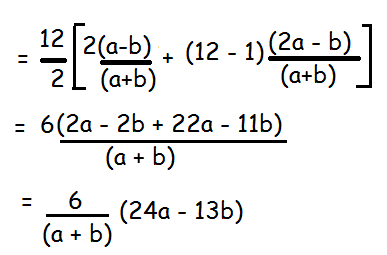
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Specifying Units of Measure
Dec 15, 25 07:09 PM
Specifying Units of Measure -
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems