ASCENDING AND DESCENDING ORDER OF FRACTIONS WORKSHEET

Problem 1 :

Place these fractions in ascending order:

1/8, -2/3, 3/11, -1/6, -3/4

Problem 2 :

Place these fractions in ascending order:

-4/5, -1  1/3, 1/2, -1/10, 5/6

Problem 3 :

Place these fractions in ascending order:

-3/4, 1  1/4, 2/3, -1  1/2, 4/5

Problem 4 :

• Jenny had a pizza that was divided into 8 equal slices. She ate 3 of them.
• Danny has a pizza that is the same size, but his is divided into 4 equal slices. He ate 3 slices of his pizza. 

Who ate more pizza?

Problem 5 :

Kim made two pies that were exactly the same size. The first pie was a cherry pie, which she cut into 6 equal slices.

The second was a pumpkin pie, which she cut into 12 equal pieces. Kim takes her pies to a party. People eat 3 slices of cherry pie and 6 slices of pumpkin pie.

Did people eat more cherry pie or pumpkin pie?

Problem 6 :

Jarred has two cakes that are the same size. The first cake was chocolate, which he cut 12 equal parts.

The second cake was marble, which he cut into 6 equal parts. His family eats 5 slices of chocolate cake and 3 slices of marble cake.

Did they eat more chocolate cake or marble cake?

Problem 7 :

Pedro and Natalia play the trumpet. Pedro practiced 3/4 of an hour last night. Natalia practiced for 1/2 an hour. Who practiced longer?

Problem 8 :

There are two piles of firewood in the backyard. The first pile has 1/2 of a cord of wood. The second pile has 3/8 of a cord of wood. Which pile has more wood?

1. Solution :

LCM of (8, 3, 11, 6, 4)

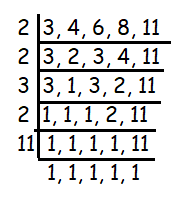
LCM  =  264

1/8  =  (1/8) ⋅ (33/33)  ==>  33/264

-2/3  =  (-2/3) ⋅ (88/88)  ==>  -176/264

3/11  =  (3/11) ⋅ (24/24)  ==>  72/264

-1/6  =  (-1/6) ⋅ (44/44)  ==>  -44/264

-3/4  =  (-3/4) ⋅ (66/66)  ==>  -198/264

Arranging the equivalent fractions in ascending order.

-198/264, -176/264, -44/264, 33/264, 72/264

Arranging corresponding fractions of equivalent fractions in ascending order, we get

-3/4, -2/3, -1/6, 1/8, 3/11

2. Solution :

LCM of (3, 2, 5, 6, 10)

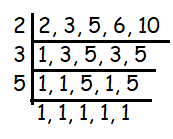
LCM  =  30

-4/5  =  (-4/5) ⋅ (6/6)  ==>  -24/30

-4/3  =  (-4/3) ⋅ (10/10)  ==>  -40/30

1/2  =  (1/2) ⋅ (15/15)  ==>  2/30

-1/10  =  (-1/10) ⋅ (3/3)  ==>  -3/30

5/6  =  (5/6) ⋅ (5/5)  ==>  25/30

Arranging the equivalent fractions in ascending order.

-40/30, -24/30, -3/30, 2/30, 25/30

Arranging corresponding fractions of equivalent fractions in ascending order, we get

-4/3, -4/5, -1/10, 1/2, 5/6

3. Solution :

LCM of (2, 3, 4, 5)

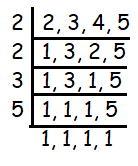
LCM  =  60

-3/4, 1  1/4, 2/3, -1  1/2, 4/5

-3/4  =  (-3/4) ⋅ (15/15)  ==>  -45/60

5/4  =  (5/4) ⋅ (15/15)  ==>  75/60

2/3  =  (2/3) ⋅ (20/20)  ==>  40/60

-3/2  =  (-3/2) ⋅ (30/30)  ==>  -90/60

4/5  =  (4/5) ⋅ (12/12)  ==>  48/60

Arranging the equivalent fractions in ascending order.

-90/60, -45/60, 40/60, 48/60, 75/60

Arranging corresponding fractions of equivalent fractions in ascending order, we get

-3/2, -3/4, 2/3, 4/5, 5/4

4. Solution :

Jenny :

Number of equal slices = 8

Number of slices she ate = 3

Fraction part of pizza Jenny ate = 3/8

Danny :

Number of equal slices = 4

Number of slices he ate = 3

Fraction part of pizza Danny ate = 3/4

Making the denominators same,

LCM of 3 and 8 is 8.

= (3/4) x (2/2)

= 6/8

Comparing 3/8 and 6/8, 6/8 is the greater fraction. So, Danny ate more pizzas.

5. Solution :

Cherry pie is curt into 6 slices and Pumpkin pie is divided into 12 equal slices.

Part of slices ate in cherry pie = 3/6

Part of slices ate in pumpkin pie = 6/12

Making the denominators same,

3/6 = (3/6) x (2/2)

= 6/12

So, same amount of each pie is eaten.

6. Solution :

Number of equal slices of chocolate cake = 12

Number of equal slices of marble cake = 6

Number of slices eaten in chocolate cake = 5

Part of slices eaten in chocolate cake = 5/12  ----(1)

Number of slices eaten in marble cake = 3

Part of slices eaten in marble cake = 3/6 -----(2)

Comparing (1) and (2),

they don't have the same denominator, making the denominator of 3/6 as denominator of 12.

= (3/6) x (2/2)

= 6/12

Now comparing the fractions 5/12 and 6/12, 6/12 is the larger fraction. So, we decide that they ate more marble cake.

7. Solution :

Time spent by Pedro = 3/4

Time spent by Natalia = 1/2

To know who has practiced longer, we have to make the denominators same.

LCM of 4 and 2 is 4.

= (1/2) x (2/2)

= 2/4

Now comparing the fractions 3/4 and 2/4, 3/4 is the greater fraction. So Pedro has practiced more.

8. Solution :

Quantity of cord of wood in 1st pile = 1/2

Quantity of cord of wood in 2nd pile = 3/8

Converting the denominators same, 

= (1/2) x (4/4)

= 4/8

Comparing the fractions 4/8 and 3/8, 4/8 is the greater fraction. So, we decide that first pile has more wood.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.