AUXILIARY LINE

Auxiliary line (Helping line) is an extra line needed to complete a proof or problem in plane geometry. 

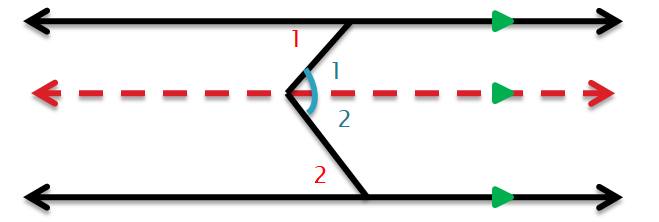
In the figure above, dotted line is an auxiliary line. Through any point there is exactly one line that will be parallel to an already existing line.   

Proving the Triangle Sum Theorem Using an Auxiliary Line

Given : ΔABC

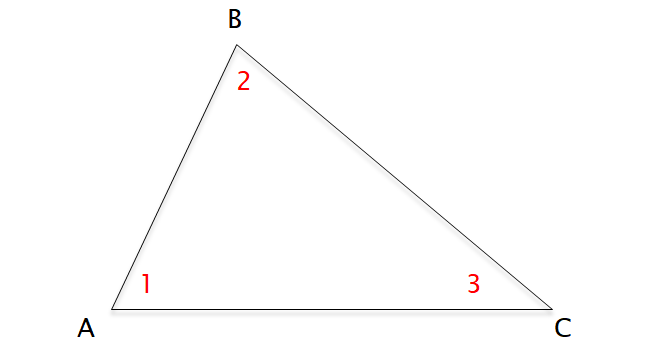
Prove : m∠1 + m∠2 + m∠3  =  180°

Recall : The sum of the interior angles of a triangle 180°.

Plane for the proof : 

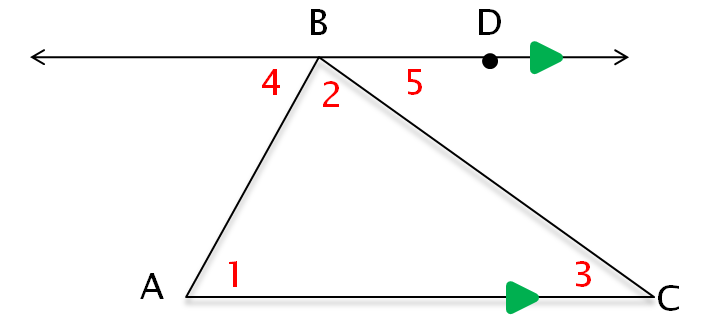
Draw an auxiliary line through B that is parallel to AC, name the new angles on this line m∠4 and m∠5.

Demonstrate that m∠4 + m∠2 + m∠5 = 180°, 

m∠1 ≅ m∠4  and  m∠3 ≅ m∠5

Use substitution to get 

m∠1 + m∠2 + m∠3  =  180°

Solved Problems

Problem 1 :

Using a 3^rd parallel Line – Auxiliary Line, find the value of x. 

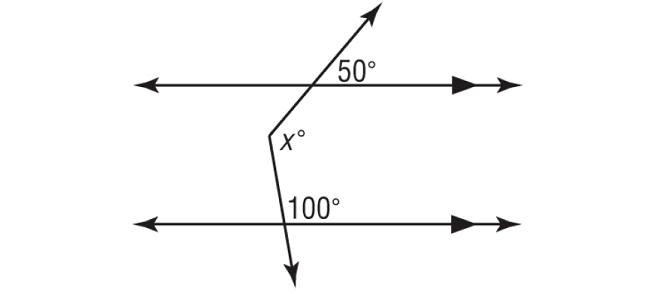
Solution :

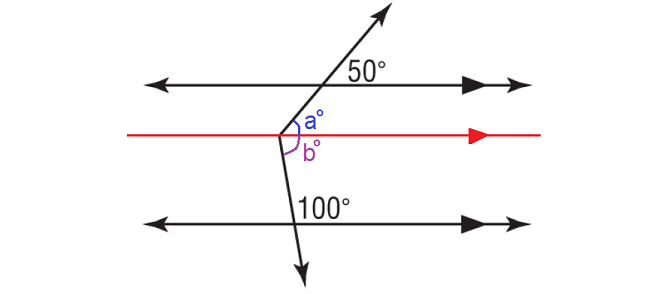
In the figure above, a° and 50° are corresponding angles and they are equal.

a°  =  50°

b° and 105° are interior angles on the same side of the transversal and they are supplementary. 

b° + 100°  =  180°

Subtract 100° from each side. 

b°  =  80°

In the above figure, 

x  =  a + b

=  50 + 80

=  130

Problem 2 :

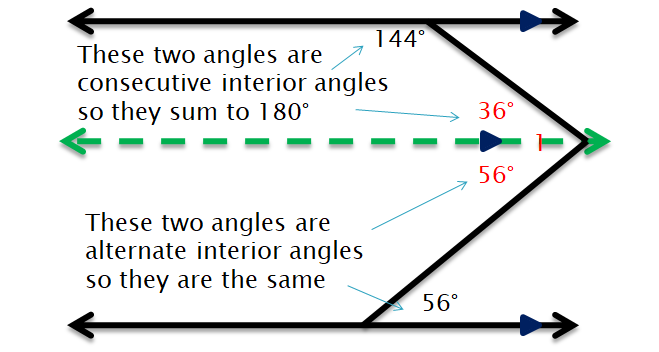
Using a 3^rd parallel Line – Auxiliary Line, find the value of x. 

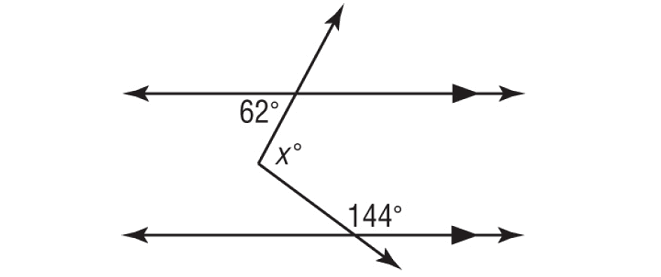
Solution :

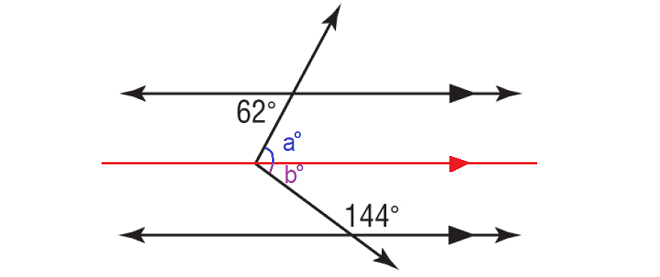
In the figure above, a° and 60° are alternate interior angles and they are equal.

a°  =  62°

b° and 144° are interior angles on the same side of the transversal and they are supplementary. 

b° + 144°  =  180°

Subtract 144° from each side. 

b°  =  36°

In the above figure,

x  =  a + b

=  62 + 36

=  98

How do we use auxiliary lines to find missing angles? Compare and contrast diagrams a and b versus diagram c.

Problem 3 :

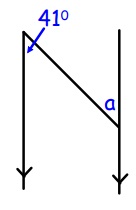
Solution :

Since the lines are parallel, alternate interior angles are equal.

a = 41

Problem 4 :

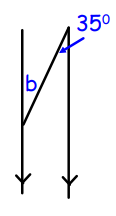
Solution :

Since the lines are parallel, alternate interior angles are equal.

b = 35

Problem 5 :

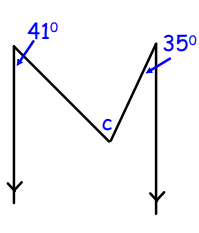
Solution :

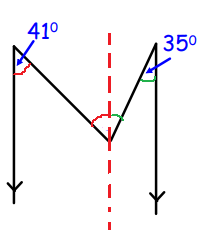
c = 41 + 35

= 76

So, the angle c is 76.

Problem 6 :

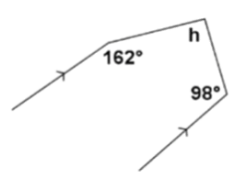
Solution :

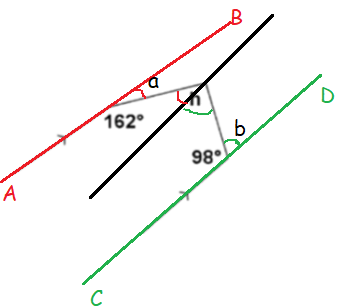
From the picture given, the lines AB and CD are parallel.

h = a + b

h = 18 + 82

h = 100

So, the value of h is 100 degree.

Problem 7 :

Find the value of the variable(s) in each figure. Explain your reasoning.

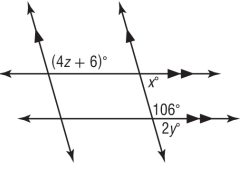
Solution :

By observing the picture above, the lines are parallel.

Sum of co-interior angles is equal to 180 degree.

x + 106 = 180

x = 180 - 106

x = 74 degree

Sum of angles of linear pair is 180 degree.

106 + 2y = 180

2y = 180 - 106

2y = 74

y = 74/2

y = 37

Corresponding angles are equal. Then,

4z + 6 = 2y

4z + 6 = 74

4z = 74 - 6

4z = 68

z = 68/4

= 17

So, the values of x, y and z are 74, 34 and 17 respectively.

Problem 8 :

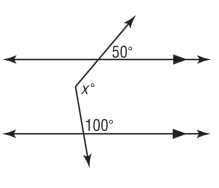
Solution :

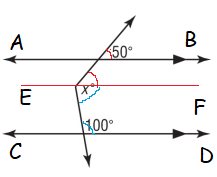
By observing the lines AB and CD are parallel.

EF is the auxiliary line.

• The angles marked using red color is co-interior angles. The sum of co-interior angles is equal to 180 degree.

So, the missing angle marked using red color is 130 (180 - 50) degree.

• The angles marked using blue color is co-interior angles. The sum of co-interior angles is equal to 180 degree.

So, the missing angle marked using blue color is 80 (180 - 100) degree.

x = 130 + 80

= 210

Problem 9 :

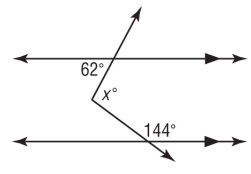
Solution :

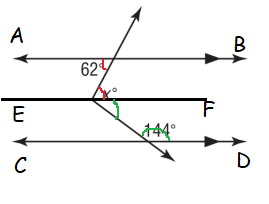
By observing the lines AB and CD are parallel.

EF is the auxiliary line.

• The angles marked using red color is alternate interior angles. So, the missing angle using red color is 62 degree.

• The angles marked using green color is co-interior angles. The sum of co-interior angles is equal to 180 degree.

= 180 - 144

= 36

x = 62 + 36

x = 98

So, the value of x is 98 degree.

Problem 10 :

A diagonal brace strengthens the wire fence and prevents it from sagging. The brace makes a 50° angle with the wire as shown. Find the value of the variable

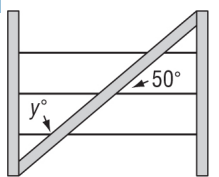
Solution :

So, missing angle is 50 degree

Problem 11 :

An auxillarv line is a new parallel line that can help us find unknown angles

Steps

1. Draw an auxiliary line through the unknown angle.

2. Use the properties of parallel lines to find the missing angles.

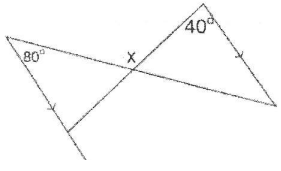
Solution :

Through x, we should draw the line.

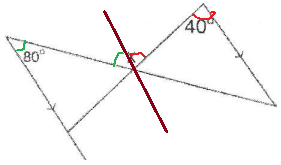
Angles marked with red color = 40

Angle marked with green = 80

x = 40 + 80

= 120 degree.

So, the angle measure x is 120 degree.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.