AVERAGE VELOCITY

If s = s(t) corresponds to the position of an object at time t, the slope of the secant line joining two points on the curve s = s(t) corresponds to the average velocity of the object.

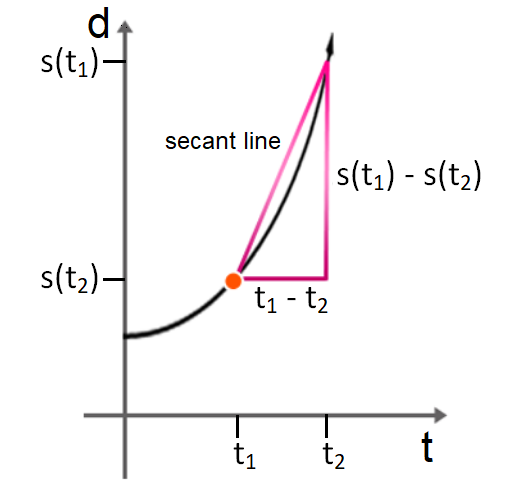
Let s₁ be the position of an object at time t₁ and s₂ be the position of the same object time t₂, then the average velocity over the time interval (t₂ - t₁) is defined by

=  change in position / change in time

=  [s(t₂) - s(t₁)] / (t₂ - t₁)

or 

Average velocity : 

=  Displacement / Time elapsed

Displacement : Distance between the starting and ending point.

Time elapsed : Total time taken. 

Example 1 :

An object moves along a straight line so that its position in meters is given by s(t) = t³ - 6t² + 9t for all time in t seconds. Find the average velocity of the object between t = 2 and t = 5 seconds.

Solution :

The average velocity between t = 2 and t = 5 is given by

=  [s(5) - s(2)] / (5 - 2)

=  [s(5) - s(2)] / 3

s(5) = 5³ - 6(5)² + 9(5) = 20

s(2) = 2³ - 6(2)² + 9(2) = 2

=  (20 - 2)/3

=  18/3

=  6 m/s

Example 2 :

The position of a car is given by s = 10 + 5t + 20t² meters at t seconds. What is the average velocity between t = 0 and t = 10 seconds?

Solution :

The average velocity between t = 0 and t = 10 is given by

=  [s(10) - s(0)] / (10 - 0)

=  [s(10) - s(0)] / 10

s(10) = 10 + 5(10) + 20(10)² = 2060

s(0) = 10 + 5(0) + 20(0)² = 10

=  (2060 - 10)/10

=  2050/10

=  205 m/s

Example 3 :

An object is dropped from the observation deck of the CN tower so that its height in meters is given by

h(t) = 447 - 4:9t²

where t is measured in seconds (we are neglecting air resistance). What is the average velocity between t = 1 and t = 2 seconds?

Solution :

The average velocity between t = 1 and t = 2 is given by

=  [h(2) - h(1)] / (2 - 1)

=  [h(2) - h(1)] / 1

=  h(2) - h(1)

h(2) = 447 - 4:9(2)² = 427.4

h(1) = 447 - 4:9(1)² = 442.7

=  427.4 - 442.7

=  -15.3

=  -15.3 m/s

Example 4 :

A car travels along a straight road to the east for 120 meters in 4 seconds, then go to the west for 40 meters in 1 second. Determine average velocity.

Solution :

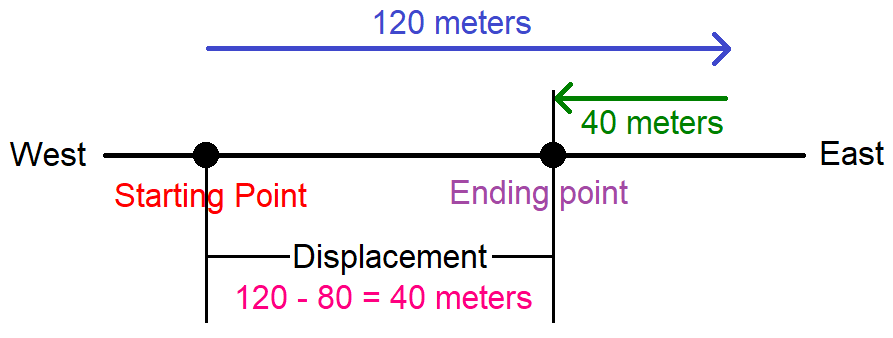
Average Velocity :

=  Displacement / Time elapsed

=  (120 - 40)/(4 + 1)

=  80/5

=  16 m/s

Example 5 :

A car travels along a straight road to the east for 40 meters in 1 second, then go to the west for 150 meters in 4 seconds. Determine average velocity.

Solution :

Average Velocity :

=  Displacement / Time elapsed

=  (150 - 40)/(1 + 4)

=  110/5

=  22 m/s

Example 6 :

A truck driver drives 20 km down the road in 5 minutes. He then reverses and drives 12 km back down the road in 3 minutes. What is his average velocity?

Solution :

Average Velocity :

=  Displacement / Time elapsed

=  (20 - 12)/(5 + 3)

=  8/8

=  1 km/min

Example 7 :

A runner is running around rectangle track with length = 50 meters and width = 20 meters. He travels around rectangle track twice, finally running back to starting point. If the total time he takes to run around the track is 100 seconds, determine average speed and average velocity.

Solution :

The perimeter of the rectangle is the distance travelled in one round. That is

=  2(50 m) + 2(20 m)

=  100 m + 40 m

=  140 meters

Runner runs around the rectangle twice and the distance covered :

=  2(140 m)

=  280 meters

He has completed two rounds around the rectangle and now he is at the starting point. 

Then the displacement = 0 meters. 

Average Velocity :

=  Displacement / Time elapsed

=  0/100

=  0 m/s

Example 8 :

A man starts walking from a point on a circular field of radius 0.5 km and 1 hour later he finds himself at the same point where he initially started. 

Solution :

If the man walks around in a circle and comes back to the same point where he started in a circle, then the change in his position is zero and the displacement is also zero. 

Average Velocity :

=  Displacement / Time elapsed

=  0/1

=  0 km/hr

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.