BASIC PROPORTIONALITY THEOREM PRACTICE QUESTIONS WORKSHEET

(1)  In ΔABC, D and E are points on the sides AB and AC respectively such that DE ∥ BC

(i) If AD/DB = 3/4 and AC = 15 cm find AE.     Solution    

(ii) If AD = 8x −7 , DB = 5x −3 , AE = 4x −3 and EC = 3x −1  find the value of x.     Solution

(2)   ABCD is a trapezium in which AB || DC and P,Q are points on AD and BC respectively, such that PQ || DC if PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD

Solution

(3)  In ΔABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DE ||BC

(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm.

(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm.

Solution

(4)  In fig. if PQ || BC and PR || CD prove that

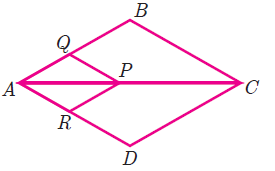
(i)  AR/RD  =  AQ/AB

(ii)  QB/AQ  =  DR/AR            Solution

(5)  Rhombus PQRB is inscribed in ΔABC such that ÐB is one of its angle. P, Q and R lie on AB, AC and BC respectively. If AB = 12 cm and BC = 6 cm, find the sides PQ, RB of the rhombus

Solution

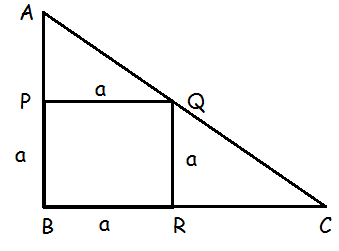
(6)  In trapezium ABCD, AB || DC , E and F are points on non-parallel sides AD and BC respectively, such that EF || AB . Show that AE/ED  =  BF/FC

Solution

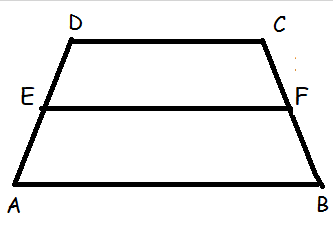
(7)  In figure DE || BC and CD || EF. Prove that AD² = AB×AF

Solution

(8)  In ΔABC, AD is the bisector of <A meeting side BC at D, if AB = 10 cm, AC = 14 cm and BC = 6 cm, find BD and DC

Solution

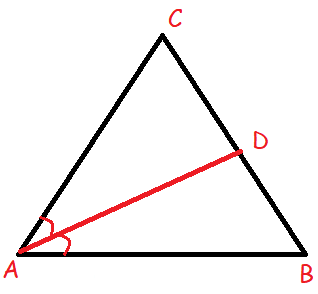
(9)  Check whether AD is bisector of <A of ΔABC in each of the following 

(i) AB = 5 cm, AC = 10 cm, BD = 1.5 cm and CD = 3.5 cm.

(ii) AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm.

Solution

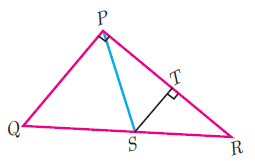
(10)  In figure <QPR = 90° , PS is its bisector. If ST ⊥ PR,  prove that ST × (PQ + PR) = PQ × PR.

Solution

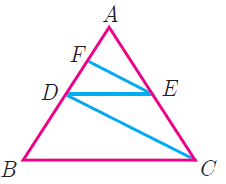
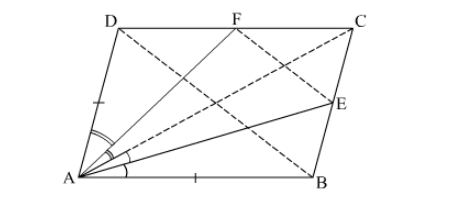
(11)  ABCD is a quadrilateral in which AB=AD, the bisector of  <BAC and <CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF  BD .

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.