BASIC TRIGONOMETRIC IDENTITIES WORKSHEET

Problem 1 : 

If p = sinθ + cosθ, q = sinθ - cosθ, then find the value of

(p² + q²)

Problem 2 : 

If x = secθ + tanθ, q = secθ + tan θ, then find the value of

xy

Problem 3 : 

If a = cscθ + cotθ, b = cscθ - cotθ, then find the value of

(a² - b²)

Problem 4 : 

Prove that 

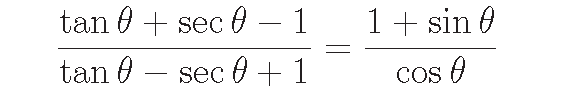
Problem 5 : 

Prove that 

(secA - cosecA)(1 + tanA + cotA)  =  tanAsecA - cotA cosecA

Problem 6 : 

Eliminate θ from

acosθ  =  b

csinθ  =  d

where a, b, c and d are constants.

Answers

Problem 1 : 

If p = sinθ + cosθ, q = sinθ - cosθ, then find the value of

(p² + q²)

Solution :

p² + q²  =  (sinθ + cosθ)² + (sinθ - cosθ)²

p² + q²  =  (sin²θ + cos²θ + 2sinθcosθ) + (sin²θ + cos²θ - 2sinθcosθ)

p² + q²  =  sin²θ + cos²θ + 2sinθcosθ + sin²θ + cos²θ - 2sinθcosθ

p² + q²  =  2sin²θ + 2cos²θ

p² + q²  =  2(sin²θ + cos²θ)

p² + q²  =  2(1)

p² + q²  =  2

Problem 2 : 

If x = secθ + tanθ, q = secθ + tan θ, then find the value of 

xy

Solution :

xy  =  (secθ + tanθ)(secθ - tanθ)

xy  =  sec²θ - tan²θ

xy  =  1

Problem 3 : 

If a = cscθ + cotθ, b = cscθ - cotθ, then find the value of

(a² - b²)

Solution :

a² - b²  =  (cscθ + cotθ)² - (cscθ - cotθ)²

a² + b²  =  (csc²θ + cot²θ + 2cscθcotθ) - (csc²θ + cot²θ - 2cscθcotθ)

a² + b²  =  csc²θ + cot²θ + 2cscθcotθ - csc²θ - cot²θ + 2cscθcotθ

a² - b²  =  4cscθcotθ

Problem 4 : 

Prove that 

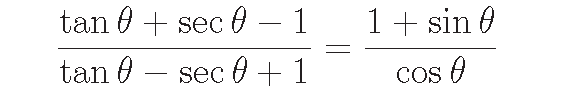
Solution :

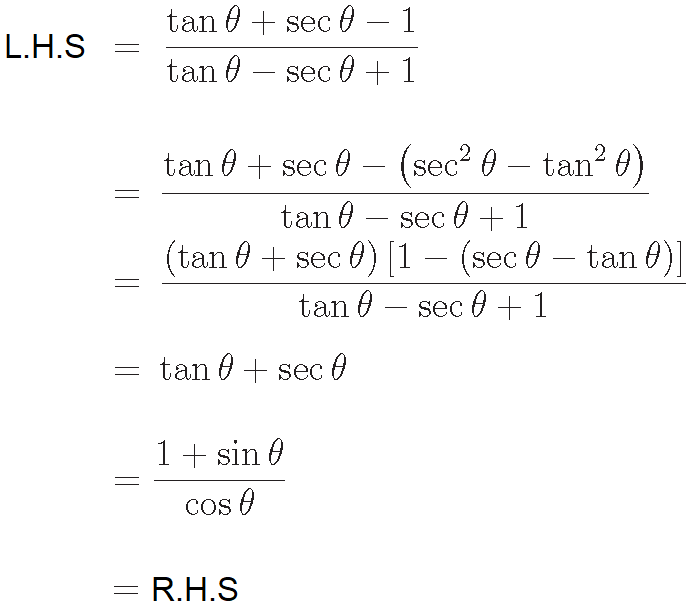
Problem 5 : 

Prove that 

(secA - cosecA)(1 + tanA + cotA)  =  tanAsecA - cotA cosecA

Solution :

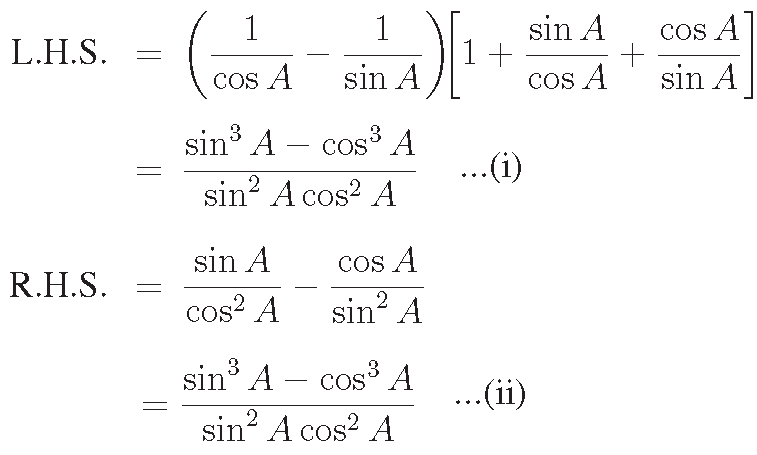
From (i) and (ii), we get the required result.

Problem 6 : 

Eliminate θ from

acosθ  =  b

csinθ  =  d

where a, b, c and d are constants.

Solution :

acosθ  =  b

Multiply each side by c. 

accosθ  =  bc

Square each side. 

(accosθ)²  =  (bc)²

a²c²cos²θ  =  b²c² -----(1)

csinθ  =  d

Multiply each side by a. 

acsinθ  =  ad

Square each side. 

(acsinθ)²  =  (ad)²

a²c²sin²θ  =  a²d² -----(2)

Add (1) and (2). 

a²c²cos²θ + a²c² sin²θ  =  b²c²  +  a²d²

a²c²(cos²θ + sin²θ)  =  b²c²  +  a²d²

a²c²(1)  =  b²c²  +  a²d²

a²c²  =  b²c²  +  a²d²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.