BIJECTIVE FUNCTION

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Let f : A ----> B be a function.

The function f is called as one to one and onto or a bijective function, if f is both a one to one and an onto function

More clearly,

f maps distinct elements of A into distinct images in B and every element in B is an image of some element in A.

The figure shown below represents a one to one and onto or bijective function.

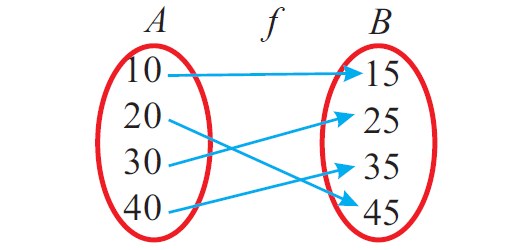
Solved Problems

Problem 1 :

Let f : A ----> B. A, B and f are defined as

A = {1, 2, 3, 4}

B = {5, 6, 7, 8}

f = {(1, 8), (2, 6), (3, 5), (4, 7)}

Verify whether f is a function. if so, what type of function is f ?

Solution :

Write the elements of f (ordered pairs) using arrow diagram as shown below.

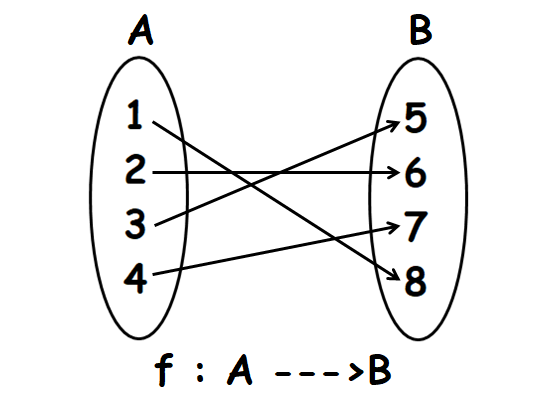
In the above arrow diagram, all the elements of A have images in B and every element of A has a unique image.

That is, no element of A has more than one image.

So, f is a function.

Every element of B has a pre-image in A. So f is onto function.

Every element of A has a different image in B.

That is, no two or more elements of A have the same image in B.

Therefore, f is one to one and onto or bijective function.

Problem 2 :

Let f : X ----> Y. X, Y and f are defined as

X = {a, b, c, d}

Y = {d, e, f}

f = {(a, e), (b, f), (c, e), (d, d)}

Is f biective ? Explain.

Solution :

Write the elements of f (ordered pairs) using arrow diagram as shown below.

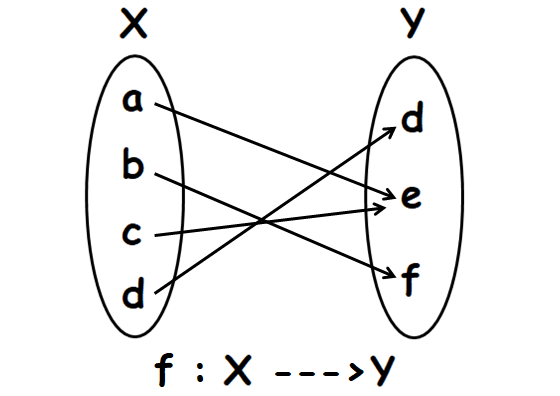
In the above arrow diagram, all the elements of X have images in Y and every element of X has a unique image.

That is, no element of X has more than one image.

So, f is a function.

Every element of Y has a pre-image in X. So f is onto function.

The elements 'a' and 'c' in X have the same image 'e' in Y.

Because the elements 'a' and 'c' have the same image 'e', the above mapping can not be said as one to one mapping.

So, f is not bijective.